INTEGERS

Summary
An integer is defined as the number that can be written without a fractional components ie,21, 4, 0, and −2048.A number which is not a fraction is a whole number that can be positive, negative , or zero.
- Z is a Subset of the set of all rational numbers
- Q, which in turn is a subset of the real numbers R.
- The symbol z can be to denote various sets
- Symbol z0+ is denoted for the positive integer
- Z0-is denoted for the negative integer.
Example

Natural numbers are positive integers
Natural numbers and “0” together termed as Whole numbers
Integers include whole numbers as well as negative integer.
Multiplication of Integers.
Multiplication of a positive integer by a positive integer: If a sign is not attached to a number, it is considered to be positive.
Example
Bharath bought 3 pencil boxes from a shop. If each box contains 6 pencils, find the total number of pencils Bharatha has?
6+ 6 + 6 = 18 (addition).
Multiplication of a Positive integer by a Negative integer
If we multiply two integers having unlike signs then, their product will be always negative.
Example
(-3)x(+4)=-12.
Multiplication of an integer by ‘0’
When an integer is multiplied by zero we get zero.
Example:
5 × 0 = 0
Multiplication of a Negative integer by a negative integer.
Here the product of two negative integers is a positive integer.
Example:
(-5)x-(6)=+30.
Division of Integer
Division of whole numbers is an inverse process of multiplication.
Exercise 1.1
Simplify the following
1) 8 + 5
= +13
2) 2 + (–7)
+7 -2
= -5
3) (–3) + (4)
4-3
= +1
4) (– 7) + (– 2)
-7 + 2
= -9
Exercise 1.2
I.Multiply each number in the row by the numbers in the column and write the product as shown.
| x | –3 | 6 | 11 | -5 |
| 7 | -21 | 42 | 77 | -35 |
| 4 | -12 | 24 | 44 | -20 |
| -8 | +24 | -48 | -88 | +40 |
| -2 | +6 | -12 | -22 | +10 |
| 12 | -36 | 72 | 132 | -60 |
| -9 | +27 | -54 | -99 | +45 |
| -4 | +42 | -84 | -154 | +70 |
II.Multiply the number in the outer circle by the number in the inner circle and fill in the appropriated boxes given outside the circle by their product.
Now select any numbers from the 8 5 -5 -6 7 -2 1 wheel and multiply by other number.

Exercise 1.3
I. Find the products of the following integers.
1)5, (– 3)
+15 x -3
= -15
2)(– 3), 8
-3 x 8
=-24
3) 7, (– 34)
7 x -34
=-238
4) (–3), (– 12)
-3 x -12
=+36
5) (– 21), 6
-21 x 6
=-126
6) (–2), (3), –(4)
-2 x3 x -4
=-6 x -4
=+24
7) (–3), 4, (–5), (–1)
-3 x 4 (-5) (-1)
= -12 x-5 x -1
-12 x +5
=-60
II. Fill in the blanks appropriately and write the product
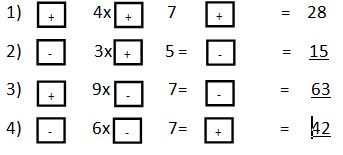
III. Tick the correct answer in the following situations.
1.An open tank filled with water is on the terrace of a building. Evaporation causes the height of the water level to change by 2cm each day.
If the first day the water level is x cm, then after 6 days the level is
a) x cm + (2 × 6) cm b) x cm – (2 × 6) cm
c) x cm – (2 × –6) cm d) 6 × x cm – 2 cm
Ans:b) x cm – (2 × 6) cm
2) During the past 8 weeks Mr. Girish has deposited 7500 each week to his bank account. He has a bank balance of 62000 now. So his bank balance 8 weeks ago if no interest is added up in this period was,
a) (62000 – 8 × 7 × 7500) b) (62000 – 8 × 7500)
c) (62000 + 8 × 7500) d) (8 × 7500 – 62000)
Ans:b) (62000 – 8 × 7500)
Exercise 1.4
I. Simplify the following.
1)(– 40) ÷ (– 10)
-40 ÷ -10
=+4
2) 34 ÷ (– 2)
34÷ -2
=-2
3) (-44) ÷ 4
-44÷4
= -11
4) (-28) ÷ (-7)
-28 ÷ -7
= +4
5)0 ÷ (-8)
0÷ -8
=-0
II. Fill in the blanks
1.(– 45) ÷1 = -45
2)(– 27) ÷ (– 27) = 1
3)30 ÷ -2 = -15
4)-12÷ 4 = -3
5)-30÷ (-3) =10
II. Fill this table.
| Division of Integers | Quotient |
| 24 ÷ 12 | +2 |
| 24 ÷ (–12) | -2 |
| (–24) ÷ 12 | -2 |
| (–24) ÷ (–12) | +2 |
Commutative Property
For any two Integers a and b, if a+ b = b +a then, this property is called commutative property.
Exercise1.5
I. Simplify the following using appropriate property.
1)5 × [(–4) + 2]
5 x (-4) + 2
5x -4 +2
5x-2
Ans:=-10
2) (-3) x (8-5)
-3 x 8-5
-3 x +3
Ans:=-9
3)(4 x (-2) ) + (5 x (-2 )
(4 x (-2 ) + (5 x (2)
4 x -2 + 5×2
-8 +10
Ans:=-18
4)(5 + (-3 ) ) -2
5+ (-3 ) -2
5 + -3 -3
2 – 2
Ans:=0
5) (-7 ) + (8-3)
-7 + 5
Ans: =-2
6)(7 x ( 2 ) ) + (4 – 7 ) -6 (2 x (-3)
14 + 4 – 7 – 12 x 3
14 + 3 – 36
17 – 36
Ans:=19
Exercise 1.6
Solve the following Verbal Problems
1.Monika had 5 boxes of chocolates
Each box contains 25 chocolates
There fore the total number of chocolates is 25 x 5
=Ans:125
3.Rashmi had 12350 in her bank account. If she withdrew 200 from her account 3 times, What is the balance amount in her account?
The amount Rashmi had in the bank account = 12,350
Rashmi withdrew 200 from her account 3 times
200 x3 = 600
Her balance in account is =11,750
4.The cost of a pen is `8 and the cost of a pencil is 5. Find the cost of a dozen pens and half a dozen pencils.
The cost of a pen is 8 x 12 = 96
The cost of a pencil is 5 x 6 =30
Therefore the cost of pen and pencil is 96 + 30
Ans:126
5.There are 38 students in a class. The cost of a set of books for one student is 1235. Find the cost of books for 38 sets.
No of students in a classis 38
cost of a set of books forone student is 1235
The cost of books for 38 sets is 1235×38
=Ans:46,930