Whole Number
Solved exercise of whole numbers

Summary
The whole numbers are the part of the number system in which it includes all the positive integers from 0 to infinity. These numbers exist in the number line.
Example: 0, 11, 25, 36, 999, 1200, etc.
What is predecessor and Successor
Predecessor: The number which comes before the particular number
Example: 5 ,6,7
6 is the predecessor of 7.
Successor: The number which comes after a particular number
Example: 5,6,7
7 is the successor of 6.
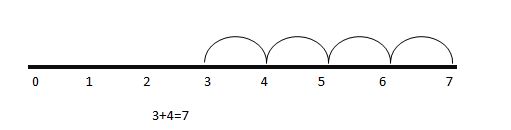
Addition on the number line:Is to add a positive number that we move the point to the right of the number line. Similarly to add a negative number implies that we move the point to the left of the number line.
Example
Subtraction on the number line:Subtraction on the number line is the subtraction of two whole numbers can also be shown on number line.
Example:

Multiplication on the number line:Multiplication of whole number on the number line.
Example

Properties of whole numbers
1. Closure property: Whole numbers are closed under addition and also under multiplication
The collection of whole number is closed under addition this property is known as closure property for addition of whole number.
Commutativity of addition and multiplication
Addition is commutation for whole numbers. This property is known as Commutativity for addition.
Ex:4+6 and 6+4
Associativity of addition and multiplication:- It states that when three or more numbers are added or multiplies the sum is the same regardless of the grouping of the addends .
Example: (2+3)+4=5+4=9
Distributivity of multiplication over addition: Can be used when you multiply a number by a sum.
Example: 3(10+2)=3(12)=36
Exercise 2.1
1. Write the next three natural numbers after 10999.
Ans:The next three natural numbers after 10999 are 11000, 11001 and 11002
2. Write the three whole numbers occurring just before 10001.
Ans:The three whole numbers occurring just before 10001 are 10000, 9999 and 9998
3. Which is the smallest whole number?
Ans:The smallest whole number is 0
4. How many whole numbers are there between 32 and 53?
Ans:The whole numbers between 32 and 53 are
(33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52)
Hence, there are 20 whole numbers between 32 and 53
5. Write the successor of: (a) 2440701 (b) 100199 (c) 1099999 (d) 2345670
The successors are
(a) 2440701 + 1 = 2440702
(b) 100199 + 1 = 100200
(c) 1099999 + 1 = 1100000
(d) 2345670 + 1 = 2345671
6. Write the predecessor of: (a) 94 (b) 10000 (c) 208090 (d) 7654321
The predecessors are
(a) 94 – 1 = 93
(b) 10000 – 1 = 9999
(c) 208090 – 1 = 208089
(d) 7654321 – 1 = 7654320
7. In each of the following pairs of numbers, state which whole number is on the left of the other number on the number line. Also write them with the appropriate sign (>, <) between them.
(a) 530, 503 (b) 370, 307 (c) 98765, 56789 (d) 9830415, 10023001
(a) Since, 530 > 503
Hence, 503 is on the left side of 530 on the number line
(b) Since, 370 > 307
Hence, 307 is on the left side of 370 on the number line
(c) Since, 98765 > 56789
Hence, 56789 is on the left side of 98765 on the number line
(d) Since, 9830415 < 10023001
Hence, 9830415 is on the left side of 10023001 on the number line.
8. Which of the following statements are true (T) and which are false (F)?
(a) Zero is the smallest natural number.
Ans:False 0 is not a natural number
(b) 400 is the predecessor of 399.
Ans:False The predecessor of 399 is 398 Since, (399 – 1 = 398)
(c) Zero is the smallest whole number.
Ans:True Zero is the smallest whole number
(d) 600 is the successor of 599.
Ans:True Since (599 + 1 = 600)
(e) All natural numbers are whole numbers.
Ans:True All natural numbers are whole numbers
(f) All whole numbers are natural numbers.
Ans:False 0 is a whole number but is not a natural number
g) The predecessor of a two digit number is never a single digit number.
Ans:False Example the predecessor of 10 is 9
(h) 1 is the smallest whole number.
Ans:False 0 is the smallest whole number
(i) The natural number 1 has no predecessor.
Ans:True The predecessor of 1 is 0 but is not a natural number
(j) The whole number 1 has no predecessor.
Ans:False 0 is the predecessor of 1 and is a whole number
(k) The whole number 13 lies between 11 and 12.
Ans:False 13 does not lie between 11 and 12
(l) The whole number 0 has no predecessor.
Ans:True The predecessor of 0 is -1 and is not a whole number
(m) The successor of a two digit number is always a two digit number.
Ans:False As the successor of 99 is 100
Exercise 2.2
1. Find the sum by suitable rearrangement:
(a) 837 + 208 + 363
(a) Given 837 + 208 + 363
= (837 + 363) + 208
= 1200 + 208
= 1408
(b) 1962 + 453 + 1538 + 647
Given 1962 + 453 + 1538 + 647
= (1962 + 1538) + (453 + 647)
= 3500 + 1100
= 4600
2. Find the product by suitable rearrangement
(a) 2 × 1768 × 50
Given 2 × 1768 × 50
= 2 × 50 × 1768
= 100 × 1768
= 176800
(b) 4 × 166 × 25
(b) Given 4 × 166 × 25
= 4 × 25 × 166
= 100 × 166
= 16600
(c) 8 × 291 × 125
Given 8 × 291 × 125
= 8 × 125 × 291
= 1000 × 291
= 291000
(d) 625 × 279 × 16
Given 625 × 279 × 16
= 625 × 16 × 279
= 10000 × 279
= 2790000
(e) 285 × 5 × 60
Given 285 × 5 × 60
= 285 × 300
= 85500
(f) 125 × 40 × 8 × 25
Given 125 × 40 × 8 × 25
= 125 × 8 × 40 × 25
= 1000 × 1000
= 1000000
3. Find the value of the following:
(a) 297 × 17 + 297 × 3
Given 297 × 17 + 297 × 3
= 297 × (17 + 3)
= 297 × 20
= 5940
(b) 54279 × 92 + 8 × 54279
Given 54279 × 92 + 8 × 54279
= 54279 × 92 + 54279 × 8
= 54279 × (92 + 8)
= 54279 × 100
= 5427900
(c) 81265 × 169 – 81265 × 69
Given 81265 × 169 – 81265 × 69
= 81265 × (169 – 69)
= 81265 × 100
= 8126500
(d) 3845 × 5 × 782 + 769 × 25 × 218
Given 3845 × 5 × 782 + 769 × 25 × 218
= 3845 × 5 × 782 + 769 × 5 × 5 × 218
= 3845 × 5 × 782 + 3845 × 5 × 218
= 3845 × 5 × (782 + 218)
= 19225 × 1000
= 19225000
4. Find the product using suitable properties.
(a) 738 × 103
(a) Given 738 × 103
= 738 × (100 + 3)
= 738 × 100 + 738 × 3 (using distributive property)
= 73800 + 2214
= 76014
(b) 854 × 102
Given 854 × 102
= 854 × (100 + 2)
= 854 × 100 + 854 × 2 (using distributive property)
= 85400 + 1708
= 87108
(c) 258 × 1008
Given 258 × 1008
= 258 × (1000 + 8)
= 258 × 1000 + 258 × 8 (using distributive property)
= 258000 + 2064
= 260064
(d) 1005 × 168
Given 1005 × 168
= (1000 + 5) × 168
= 1000 × 168 + 5 × 168 (using distributive property)
= 168000 + 840
= 168840
5. A taxi driver filled his car petrol tank with 40 litres of petrol on Monday. The next day, he filled the tank with 50 litres of petrol. If the petrol costs ₹ 44 per litre, how much did he spend in all on petrol?
Petrol quantity filled on Monday = 40 litres
Petrol quantity filled on Tuesday = 50 litres
Total petrol quantity filled = (40 + 50) litre
Cost of petrol per litre = ₹ 44
Total money spent = 44 × (40 + 50)
= 44 × 90
= ₹ 3960
6. A vendor supplies 32 litres of milk to a hotel in the morning and 68 litres of milk in the evening. If the milk costs ₹ 45 per litre, how much money is due to the vendor per day?
Milk quantity supplied in the morning = 32 litres
Milk quantity supplied in the evening = 68 litres
Cost of milk per litre = ₹ 45
Total cost of milk per day = 45 × (32 + 68)
= 45 × 100
= ₹ 4500
Hence, the money is due to the vendor per day is ₹ 4500
7. Match the following:
| 425 × 136 = 425 × (6 + 30 + 100) | Distributivity of multiplication over addition. |
| 2 × 49 × 50 = 2 × 50 × 49 | Commutativity under multiplication |
| 80 + 2005 + 20 = 80 + 20 + 2005 | Commutativity under addition |
Exercise 2.3
Which of the following will not represent zero?
(a) 1 + 0
Ans: 1 + 0 = 1 Hence, it does not represent zero
(b) 0 × 0
Ans: 0 × 0 = 0 Hence, it represents zero
(c) 0 / 2
Ans:0 / 2 = 0
Hence, it represents zero
(d) (10 – 10) / 2
Ans:(10 – 10) / 2 = 0 / 2 = 0 Hence, it represents zero
2. If the product of two whole numbers is zero, can we say that one or both of them will be zero? Justify through examples.
If product of two whole numbers is zero, definitely one of them is zero
Example: 0 × 3 = 0 and 15 × 0 = 0
If product of two whole numbers is zero, both of them may be zero
Example: 0 × 0 = 0
Yes, if the product of two whole numbers is zero, then both of them will be zero
3. If the product of two whole numbers is 1, can we say that one or both of them will be 1? Justify through examples
If the product of two whole numbers is 1, both the numbers should be equal to 1
Example: 1 × 1 = 1
But 1 × 5 = 5
Hence, its clear that the product of two whole numbers will be 1, only in situation when both numbers to be multiplied are 1
4. Find using distributive property:
(a) 728 × 101
Given 728 × 101
= 728 × (100 + 1)
= 728 × 100 + 728 × 1
= 72800 + 728
= 73528
(b) 5437 × 1001
Given 5437 × 1001
= 5437 × (1000 + 1)
= 5437 × 1000 + 5437 × 1
= 5437000 + 5437
= 5442437
(c) 824 × 25
Given 824 × 25
= (800 + 24) × 25
= (800 + 25 – 1) × 25
= 800 × 25 + 25 × 25 – 1 × 25
= 20000 + 625 – 25
= 20000 + 600
= 20600
(d) 4275 × 125
Given 4275 × 125
= (4000 + 200 + 100 – 25) × 125
= (4000 × 125 + 200 × 125 + 100 × 125 – 25 × 125)
= 500000 + 25000 + 12500 – 3125
= 534375
(e) 504 × 35
Given 504 × 35
= (500 + 4) × 35
= 500 × 35 + 4 × 35
= 17500 + 140
= 17640