QUADRILATERALS

Class 9 exercise

PARALLELOGRAM:

A parallelogram is a quadrilateral in which opposite sides are parallel.

PROPERTIES OF PARALLELOGRAM:

Theorem1: A diagonal of a parallelogram divides it into two congruent triangles.

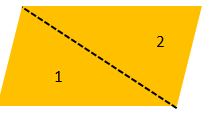
Theorem 2:The opposite sides of a parallelogram are equal.

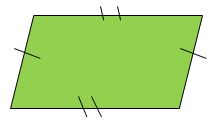
Theorem 3 : If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.

Theorem 4. The opposite angles of a parallelogram are equal

Theorem 5 : If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.

Theorem 6. The diagonals of a parallelogram bisect each other.

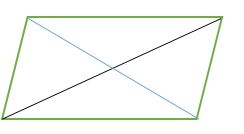
Theorem 7. The diagonals of a parallelogram bisect each other

Theorem 8. A quadrilateral is a parallelogram if a pair of opposite sides is equal and parallel.

1. The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.
Solution:

Let the angles of the quadrilateral be 3x, 5x, 9x and 13x.

∴ 3x + 5x + 9x + 13x = 360° [Angle sum property of a quadrilateral]

⇒ 30x = 360°

⇒      x = 360°/30= 12°

∴ 3x = 3 x 12° = 36°

5x = 5 x 12° = 60°

9x = 9 x 12° = 108°

13a = 13 x 12° = 156°

⇒ The required angles of the quadrilateral are 36°, 60°, 108° and 156°.

2. If the diagonals of a parallelogram are equal, then show that it is a rectangle.

Solution:Let ABCD is a parallelogram such that AC = BD.

In ∆ABC and ∆DCB,

AC = DB [Given]

AB = DC [Opposite sides of a parallelogram]

BC = CB [Common]

∴ ∆ABC ≅ ∆DCB [By SSS congruency]

⇒ ∠ABC = ∠DCB [By C.P.C.T.] …(1)

Now, AB || DC and BC is a transversal. [ ∵ ABCD is a parallelogram]

∴ ∠ABC + ∠DCB = 180° … (2) [Co-interior angles]

From (1) and (2), we have

∠ABC = ∠DCB = 90°

i.e., ABCD is a parallelogram having an angle equal to 90°.

∴ ABCD is a rectangle.