Rational Numbers
An Introduction to Number system
Summary
A set of values used to represent different quantities is known as “Number System”. For example, a number system can be used to represent the number of students or the number of viewers watching a certain TV program, the temperature of a place, height of plants, etc.
The number theory has a fundamental body of knowledge.this number theory has played a pivotal role in the development of mathematics even Pythagoras believe that everything is numbers. The number system is a system of representing numbers. The whole numbers are the original source of all mathematics.
Real Number System.

Real number System includes the
- Natural Numbers
- whole Numbers
- Integers
- Rational number
Rational Number
Rational numbers are a subset of the real numbers. Any number which can be written in the form of, P by Q, Where P and Q are integers. all the integers are rational numbers are represented by Q. If Q is equal to zero then P by Q becomes not defined.

Rational numbers include
- Natural numbers
- Whole numbers
- Integers and
- all negative and positive fractions.
Zero as a Rational Numbers
Zero divided by any integer results the rational number zero. so 0 can be written in the form of p/q. Therefore 0 is also a rational number. for example o/11, o/(-8), 0/8, 0/5 etc.
Negative and positive Rational Numbers.
If P and Q both are positive the rational number is positive. For example (7/8), (56/145), (6/1259), etc.
If p and q both are negative the rational number is positive.
For example: (-56/-65)=56/65 (as when we simplify a rational number the minus sign get cuts.
If any of p or q are negative the rational number is negative
Example: 98/(-5), (-1)/2, etc
2 1
3 4
Representation of number on the Number line
Number line can be represented on the number line according to their types.
The most ways of representing the number line are as follows:
- Natural number
- Whole numbers
- Integers
- Rational numbers
Number line of natural numbers
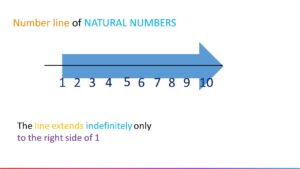
The line extends indefinitely only to the right side of 1
Number Line of Whole Numbers
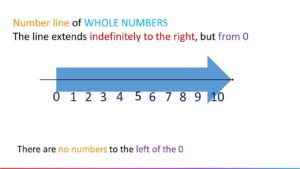
The line extends indefinitely to the right , but from 0
There are no numbers to the left of the 0
Number line of Integers.
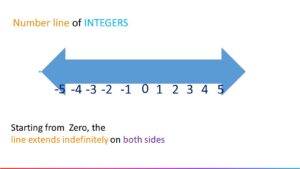
The line extends indefinitely on both the sides.
Number Line of rational Numbers
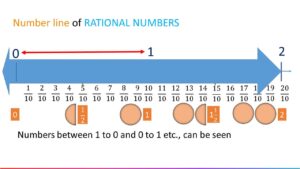
The line extends indefinitely to both the sides. But yo can now see numbers between 1,0,0,1 etc.
So, unlike natural numbers and integers, there are countless rational numbers between any two given rational numbers.
PROPERTIES OF RATIONAL NUMBERS
Properties of rational numbers lie under the four operations of arithmetic:
- Addition of rational numbers.
- Subtraction of rational numbers.
- Multiplication of rational numbers.
- Division of rational numbers.
Different Properties of rational numbers
- Closure Property
- Associative property
- Distributive property
- Additive property
- Multiplicative inverse
Closure property
Rational numbers are closed under addition. That is, for any two rational numbers a and b, a+b is also a rational numbers
For Example – 8+3 = 11 (a rational number)
a+b=c
Rational numbers are closed under subtraction. That is, for any two rational numbers a and b, a-b is also a rational numbers
For Example : 8-3 = 5 (a rational number)
a-b=c
Rational numbers are closed under Multiplication. That is, for any two rational numbers a and b, a X b is also a rational numbers
For Example : 8X3 = 24 (a rational
number)
a x b=c
Identity Property (property of 0)
Zero added to any rational numbers the number does not change. so zero is called Identity Elements for the addition of rational numbers.(0+a=a)
Additive Inverse: If the sum of two rational numbers is 0 then the two numbers are called additive inverse of each other.
For example, 2/3+(-2)3=0
COMMUTATIVE PROPERTY
Addition The sum of two rational numbers does not depend on the order in which they are added. (a+b= b+a)
for example , a=1/2 ,b=3/4
1/2+ 3/4 = 3/4 + 1/2 = 5/4 Subtraction v Rational number do not hold commutative property
Example -1
If a=1/2 and b=3/4 , verify the following i)aXb=bXa ii)a+b=b+a

COMMUTATIVE PROPERTY
Multiplication Two rational number can be multiplied in any order.
For example 1/2×3/4=3/4×1/2=3/8
Division Rational numbers do not hold these property.
Associative Property
Addition The sum of three or more rational numbers does not depend on the way they are added. (a+b)+c =a+(b+c) • a=-2/3 , b=5/7 , c=1/6.
Example 2
If a=-2/3 , b=5/7 , c=1/6 Verify that (a+b)+c= a+(b+c)
LHS={“(a+b)+c” } RHS = {a+(b+c)}
= {((-2)/3+5/7)+1/6} = {(-2)/3+(5/7+1/6)}
={((-14+15))/21+1/6} ={(-2)/3+((30+7))/42}
=(1/21+1/6) =((-2)/3+37/42)
= ((9))/42 = ((-28+37)/42)
=3/14 = 9/42
=3/14
∴LHS=RHS
Associative Property
Rational numbers do not hold associative property under subtraction. • •Multiplication: •The product of three or more numbers does not depend on the order they are multiplied in or they are grouped as.
(a+b)+c =a+(b+c)
a=-2/3 , b=5/7 , c=1/6
Multiplicative Identity
The product of any rational number with one is the number itself. so 1 is called the multiplicative identity of rational numbers.
Zero property: The product of any rational number and 0 is 0. for example: 9874561253 X 0=0
Distributive property of Multiplication over Addition and subtraction:
[ax(b+c)=axb+axc]
]ax(b-c)=axb-axc]
Show that (-8/ 9×1/-5)+-8/9x-7/11)= -8/9 x 1/-5+-7/11)

Property of Zero
Zero subtracted from any rational number leaves it unchanged and any rational number subtracted from 0 gives its additive inverse.
For example: 3/2-0=3/2
0-3/2=(-3)/2
Operation on Rational Numbers
Rational Numbers provide the first number system in which all the operations of arithmetic, addition, subtraction, multiplication, and division are possible.
Multiplication “makes a number bigger” and division “makes a number smaller”. The arithmetical operation is reduced to operations between two rational numbers.
Addition: it is the first operations .This operation uses only one sign[+].
Subtraction: it is the second operation. This operation uses only one sign[-].
Multiplication:It is often described as a sort of short hand for addition This operation uses sign[x].
Division: It is the last and an important operation. The operation uses the sign[+].
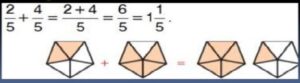
Adding Rational Numbers with Common denominators.
To add rational numbers that have a common denominator, we add the numerator, but we do not add the denominators.
For example.
Addition rational Numbers with Different Denominators.
To add rational numbers with different denominators, first, we equalize the denominators by enlarging each rational number by the “lowest common multiple”(LCM) as the denominator.then we add the numerators
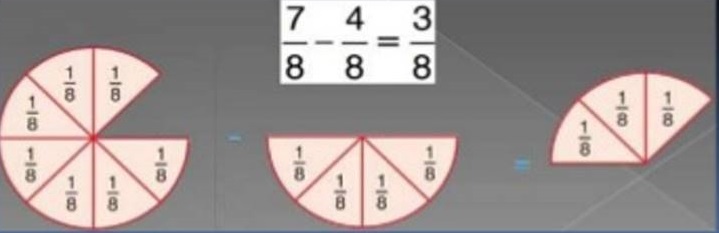
Subtracting rational Numbers with Common Denominators.
Subtraction is the inverse operation of addition.
To subtract rational numbers that have a common denominators, we subtract the numerator, but we not subtract the denominators.
For example
Subtracting rational Numbers with different denominators.
To subtract rational numbers with different denominators, first equalize the denominators by enlarging each rational numbers by the “lowest common multiple”(LCM) as the denominator.
The subtract the numerators.
Multiplying Rational Numbers
To multiply two rational numbers, we multiply the numerators to get the new numerator and multiply the denominators to get the new denominators.
For example

Division In Rational Numbers
To divide two rational numbers we take the reciprocal of the second rational number and multiply it by the first number.

Application And uses
Rational numbers are important
They are used in the real world Everyday
Even though we are not thinking about it if the number is rational or not, we still use them in our everyday lives.At school or in the kitchen. We even see them on TV.