Exponents and Powers

The exponents tells us that how many times the number should be multiplied. It is called the Exponential form. This is written like this:

10^{9 Exponent}

Here 10 is the base and 9 is the exponent and this complete number is the power. We pronounce it as 10 raised to the power 9. The exponent could be positive or negative.

This tells us that the number 10 will be multiplied 9 times, like,

10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10

Powers with Negative Exponents

The exponents could be negative also and we can convert them in positive by the following method.

This shows that for any non-zero negative integers a,

where m is the positive integer and a^m is the multiplicative inverse of a^-m.

Laws of Exponents

If we have a and b as the base and m and n as the exponents, then

Some More Examples

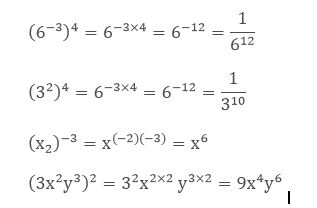
Use of Exponents to Express Small Numbers in Standard Form

Sometimes we need to write the numbers in very small or large form and we can use the exponents to represent the numbers in small numbers.

1. Standard form to write the natural numbers like xyz000000……

Step 1: First of all count the number of digits from left leaving only the first digit.
Step 2: To write it in exponent or standard form, write down the first digit.
Step 3: If there are more digits in the number then put a decimal after the first digit and then write down the other digits until the zero comes. And if there are no digits after the first digit then skip this step.

Step 4: Now place a multiplication sign and then write down the counted digits in the first step as the exponent to the base number 10.

Example:

Express 1730000000000 in exponent form.

Solution: 

In standard form, the number 1730000000000 will be written as 1.73 x 10¹².

2. Standard form to write decimal numbers like 0.00000…..xyz.

Step 1: First of all count the number of digits from the decimal point to the last digit.
Step 2: If there is only one digit after the zeros then simply write down that digit. Place a multiplication sign and write down the counted digits in step-1 with a negative sign as the exponent to base number 10.
Step 3: If there are two or more non-zero digits at the end of the number. Then, write down the digits followed by a decimal point after the first digit and the other non-zero digits.
Step 4: Now calculate the number of digits in the first step and minus the number of digits appearing after the decimal point.
Step 5: Place a multiplication sign and write down the counted digits in step-4 with a negative sign as an exponent to base number 10.

Example:

Express 0.000000000000073 in exponent form.

Solution:

In standard form, the number will be written as 7.3 x 10^-14.

Comparing Very Large and Very Small Numbers

To compare the very large or very small numbers we need to make their exponents same. When their exponents are the same then we can compare the numbers and check which number is large or small.

Example

Compare the two numbers 4.56 × 10⁸ and 392 × 10⁷.

Solution

To compare these numbers, we need to make their exponents same.

4.56 × 10⁸

392 × 10⁷ = 39.2 × 10⁸

As the exponents are the same, we can easily see that which number is larger.

392 × 10⁷ > 4.56 × 10⁸

Remark: To add and subtract also we need to make their exponents same and then they can be easily added or subtracted.

 Exercise 2.1

1.Evaluate:

(i) 3^-2                                                        (ii) (-4)^-2                                                                       (iii) ()^-5

 Solution:

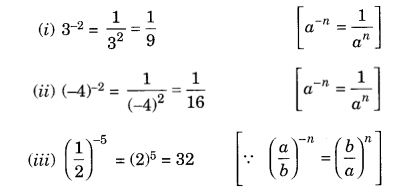
2.Simplify and express the result in power notation with a positive exponent.

Solution:

3.Find the value of

Solution:

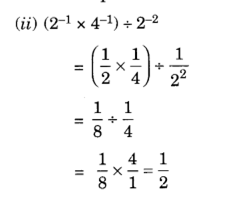
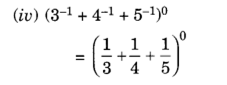
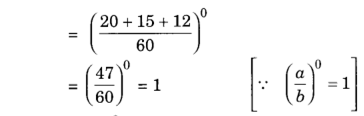
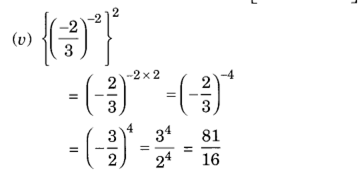
4.

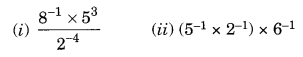
Solution:

5.Find the value of m for which 5^m ÷ 5^-3 = 5⁵.
Solution:
5^m ÷ 5^-3 = 5⁵
⇒ 5^m-(-3) = 5⁵ [∵ a^m ÷ aⁿ = a^m-n]
⇒ 5^m+3 = 5⁵
Comparing the powers of equal bases, we have
m + 3 = 5
m = 5 – 3 = 2, i.e., m = 2

6.Evaluate:

Solution:

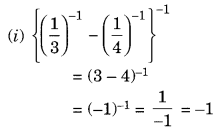
7.Simplify:

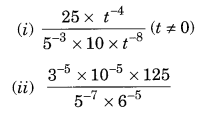
Solution:

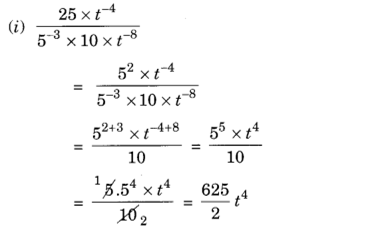
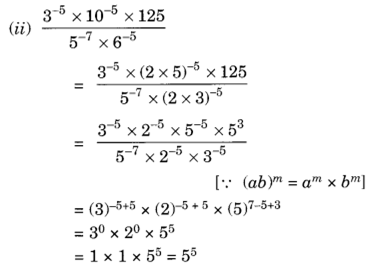
Exercise 12.2

1. Express the following numbers in standard form:
   (i) 0.0000000000085
   (ii) 0.00000000000942
   (iii) 6020000000000000
   (iv) 0.00000000837
   (v) 31860000000

Solution:

(v) 31860000000
= 3.186 × 10000000000
= 3.186 × 10¹⁰
Hence, the required standard from = 3.186 × 10¹⁰

2.Express the following numbers in usual form.
(i) 3.02 × 10^-6
(ii) 4.5 × 10⁴
(iii) 3 × 10^-8
(iv) 1.0001 × 10⁹
(v) 5.8 × 10¹²
(vi) 3.61492 × 10⁶

Solution:

1. Express the number appearing in the following statements in standard form.
   (i) 1 micron is equal to 1/1000000 m.
   (ii) Charge of an electron is 0.000,000,000,000,000,000,16 coulomb
   (iii) Size of a bacteria is 0.0000005 m
   (iv) Size of a plant cell is 0.00001275 m
   (v) Thickness of a thick paper is 0.07 mm.

Solution:

4.In a stack there are 5 books each of thickness 20 mm and 5 paper sheets each of thickness 0.016 mm. What is the total thickness of the stack?
Solution:
Thickness of books = 5 × 20 = 100 mm
Thickness of 5 paper sheets = 5 × 0.016 mm = 0.080 mm.
Total thickness of the stack = 100 mm + 0.080 mm = 100.080 mm = 1.0008 × 10² mm