The Triangle and its Properties
Solved exercise on triangle and its properties

Exercise
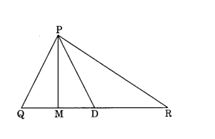
1. In ∆PQR, D is the mid-pointof QR
PM is
PD is
If QM = MR?
Solution:
PM is altitude.
PD is median.
No, QM ≠ MR.
2. Draw rough sketches for the following
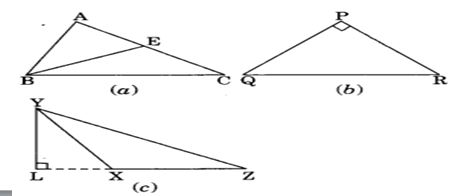
(a) In ∆ABC, BE is a median.
(b) In ∆PQR, PQ and PR are altitudes of the triangle.
(c) In ∆XYZ, YL is an altitude in the exterior of the triangle.
3. Verify by drawing a diagram if the median and altitude of an isosceles triangle can be same.
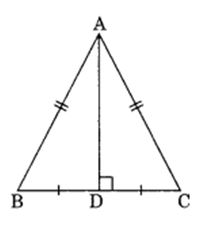
∆ABC is an isosceles triangle in which AB = AC
Draw AD as the median of the triangle.
Measure the angle ADC with the help of protractor we find, ∠ADC = 90°
Thus, AD is the median as well as the altitude of the ∆ABC. Hence Verified.
Exercise 6.2
1. Find the value of the unknown exterior angle x in the following diagrams
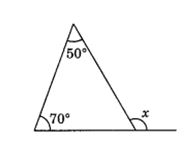
Solution
(i)∠x = 50° + 70°
= 120°
(Exterior angle is equal to sum of its interior opposite angles)
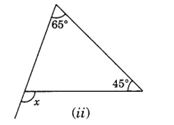
(ii) ∠x = 65°+ 45°
= 110°
(Exterior angle is equal to sum of its interior opposite angles)
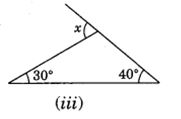
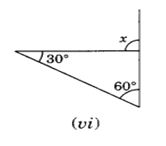
(iii) ∠x = 30° + 40°
= 70°
(Exterior angle is equal to sum of its interior opposite angles)
(iv) ∠x = 60° + 60°
= 120°
(Exterior angle is equal to sum of its interior opposite angles)
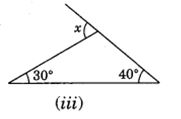
(v) ∠x = 50° + 50°
=100°
(Exterior angle is equal to sum of its interior opposite angles)
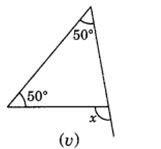
(vi) ∠x = 30° + 60°
= 90°
(Exterior angle is equal to sum of its interior opposite angle)
2. Find the value of the unknown interior angle x in the following figures:
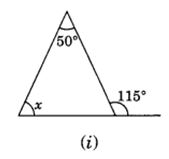
(i) ∠x + 50° = 115° (Exterior angle of a triangle)
∴ ∠x = 115°- 50° = 65°
(ii) ∠x + 70° = 110° (Exterior angle of a triangle)
∴ ∠x = 110° – 70° = 40°
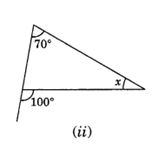
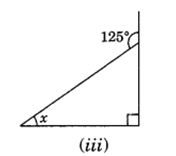
(iii) ∠ x + 90° = 125° (Exterior angle of a right triangle)
∴ ∠x = 125° – 90° = 35°
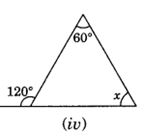
(iv) ∠x + 60° = 120° (Exterior angle of a triangle)
∴ ∠x = 120° – 60° = 60°
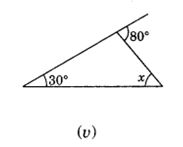
(v)∠ X + 30° = 80° (Exterior angle of a triangle)
∴ ∠x = 80° – 30° = 50°
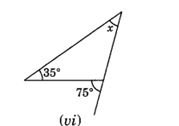
(vi) ∠ x + 35° = 75° (Exterior angle of a triangle)
∴ ∠ x = 75° – 35° = 40°
Exercise 6.3
1. Find the value of the unknown x in the following diagrams
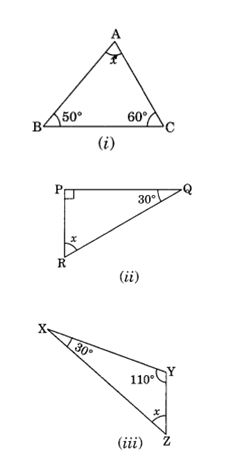
Solution:i) By angle sum property of a triangle, we have
∠x + 50° + 60° = 180°
⇒ ∠x + 110° = 180°
∴ ∠x = 180° – 110° = 70°
(ii) By angle sum property of a triangle, we have
∠x + 90° + 30 = 180° [∆ is right angled triangle]
⇒ ∠x + 120° = 180°
∴ ∠x – 180° – 120° = 60°
(iii) By angle sum property of a triangle, we have
∠x + 30° + 110° – 180°
⇒ ∠x + 140° = 180°
∴ ∠x = 180° – 140° = 40°
Find the value of the unknown x in the following diagrams
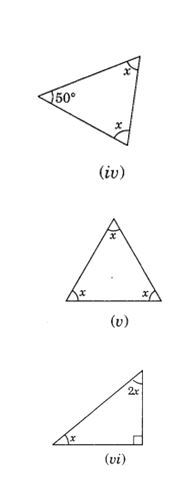
Solution:(iv ) By angle sum property of a triangle, we have
∠x + ∠x + 50° = 180°
⇒ 2x + 50° = 180°
⇒ 2x = 180° – 50°
⇒ 2x = 130°
∴ x=130/2=65∘
(v) By angle sum property of a triangle, we have
∠x + ∠x +∠x =180°
⇒ 3 ∠x = 180°
∴ ∠x=180/3=60∘
(vi) By angle sum property of a triangle, we have
x + 2 x + 90° = 180° (∆ is right angled triangle)
⇒ 3x + 90° = 180°
⇒ 3x = 180° – 90°
⇒ 3x = 90°
∴ x=90/3=30∘
2. Find the values of the unknowns x and y in the following diagrams:
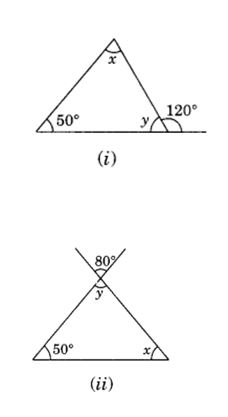
(i) ∠x + 50° = 120° (Exterior angle of a triangle)
∴ ∠x = 120°- 50° = 70°
∠x + ∠y + 50° = 180° (Angle sum property of a triangle)
70° + ∠y + 50° = 180°
∠y + 120° = 180°
∠y = 180° – 120°
∴ ∠y = 60°
Thus ∠x = 70 and ∠y – 60°
(ii) ∠y = 80° (Vertically opposite angles are same)
∠x + ∠y + 50° = 180° (Angle sum property of a triangle)
⇒ ∠x + 80° + 50° = 180°
⇒ ∠x + 130° = 180°
∴ ∠x = 180° – 130° = 50°
Thus, ∠x = 50° and ∠y = 80°
Find the values of the unknowns x and y in the following diagrams:
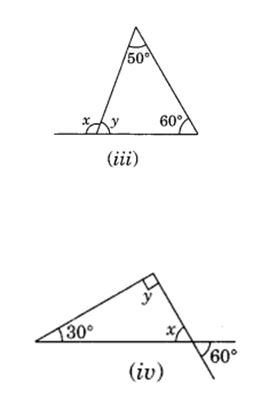
(iii) ∠y + 50° + 60° = 180° (Angle sum property of a triangle)
∠y + 110° = 180°
∴ ∠y = 180°- 110° = 70°
∠x + ∠y = 180° (Linear pairs)
⇒ ∠x + 70° = 180°
∴ ∠x = 180° – 70° = 110°
Thus, ∠x = 110° and y = 70°
(iv) ∠x = 60° (Vertically opposite angles)
∠x + ∠y + 30° = 180° (Angle sum property of a triangle)
⇒ 60° + ∠y + 30° = 180°
⇒ ∠y + 90° = 180°
⇒ ∠y = 180° – 90° = 90°
Thus, ∠x = 60° and ∠y = 90°
Find the values of the unknowns x and y in the following diagrams:
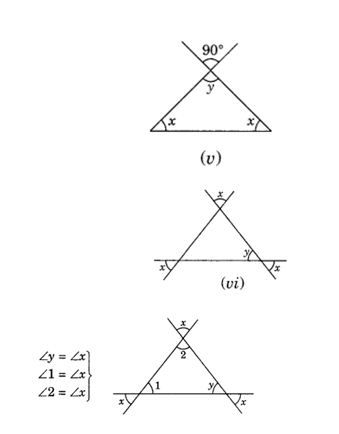
(v) ∠y = 90° (Vertically opposite angles)
∠x + ∠x + ∠y = 180° (Angle sum property of a triangle)
⇒ 2 ∠x + 90° = 180°
⇒ 2∠x = 180° – 90°
⇒ 2∠x = 90°
∴ ∠x=90/2=45∘
Thus, ∠x = 45° and ∠y = 90°
(vi) From the given figure, we have
Adding both sides, we have
∠y + ∠1 + ∠2 = 3∠x
⇒ 180° = 3∠x (Angle sum property of a triangle)
∴ ∠x=180/ 3=60∘
∠x = 60°, ∠y = 60°
Exercise 6.4 & 6.5
1. Is it possible to have a triangle with the following sides?
(i) 2 cm, 3 cm, 5 cm
(ii) 3 cm, 6 cm, 7 cm
(iii) 6 cm, 3 cm, 2 cm
Solution:We know that for a triangle, the sum of any two sides must be greater than the third side.
(i) Given sides are 2 cm, 3 cm, 5 cm
Sum of the two sides = 2 cm + 3 cm = 5 cm Third side = 5 cm
We have, Sum of any two sides = the third side i.e. 5 cm = 5 cm
Hence, the triangle is not possible.
(ii) Given sides are 3 cm, 6 cm, 7 cm
Sum of the two sides = 3 cm + 6 cm = 9 cm Third side = 7 cm
We have sum of any two sides > the third
side. i.e. 9 cm > 7 cm
Hence, the triangle is possible.
(iii) Given sides are 6 cm, 3 cm, 2 cm
Sum of the two sides = 3 cm + 2 cm – 5 cm Third side = 6 cm
We have, sum of any two sides < the third sid6 i.e. 5 cm < 6 cm Hence, the triangle is not possible.
2. Take any point O in the interior of a triangle PQR . Is
i) OP + OQ > PQ?
(ii) OQ + OR > QR?
(iii) OR + OP > RP?
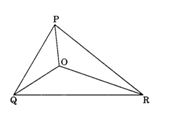
Solution:(i) Yes, In ∆ OPQ, we have
OP + OQ > PQ
[Sum of any two sides of a triangle is greater than the third side]
(ii) Yes, In ∆OQR, we have OQ + OR > QR
[Sum of any two sides of a triangle is greater than the third side]
(iii) Yes, In ∆OPR, we have OR + OP > RP
[Sum of any two sides of a triangle is greater than the third side]
3. AM is a median of a triangle ABC.
Is AB + BC + CA > 2AM ?
(Consider the sides of triangles ∆ABM and ∆AMC)
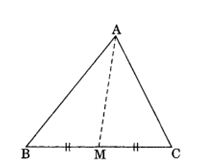
Solution:Yes, In ∆ ABM, we have
AB + BM > AM …(i)
[Sum of any two sides of a triangle is greater than the third side]
In ∆AMC, we have
AC + CM > AM …(ii)
[Sum of any two sides of a triangle is greater than the third side]
Adding eq (i) and (ii), we have
AB + AC + BM + CM > 2AM
AB + AC + BC + > 2AM
AB + BC + CA > 2AM
Hence, proved.
4. ABCD is a quadrilateral.
Is AB + BC + CD + DA > AC + BD?
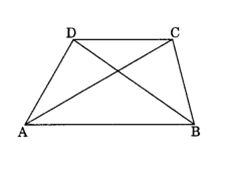
Solution:
In ∆ABC, we have
AB + BC > AC …(i)
[Sum of any two sides is greater than the third side]
In ∆BDC, we have
BC + CD > BD …(ii)
[Sum of any two sides is greater than the third side]
In ∆ADC, we have
CD + DA > AC …(iii)
[Sum of any two sides is greater than the third side]
In ∆DAB, we have
DA + AB > BD …(iv)
[Sum of any two sides is greater than the third side]
Adding eq. (i), (ii), (iii) and (iv), we get
2AB + 2BC + 2CD + 2DA > 2AC + 2BD or
AB + BC + CD + DA > AC + BD [Dividing both sides by 2]
Hence, proved.
5. ABCD is a quadrilateral.
Is AB + BC + CD + DA < 2(AC + BD)?
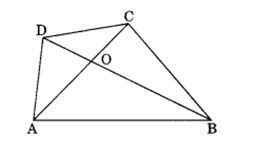
Solution:we have a quadrilateral ABCD.
In ∆AOB, we have AB < AO + BO …(i)
[Any side of a triangle is less than the sum of other two sides]
In ∆BOC, we have
BC < BO + CO …(ii)
[Any side of a quadrilateral is less than the sum of other two sides]
In ∆COD, we have
CD < CO + DO …(iii)
[Any side of a triangle is less than the sum of other two sides]
In ∆AOD, we have
DA < DO + AO …(iv)
[Any side of a triangle is less than the sum of other two sides]
Adding eq. (i), (ii), (iii) and (iv), we have
AB + BC + CD + DA
∠2AO + ∠BO + ∠CO + ∠DO
∠2(AO + BO + CO + DO)
∠2 [(AO + CO) + (BO + DO)]
∠2(AC + BD)
Thus, AB + BC + CD + DA < 2(AC + BD)
Hence, proved.
6. The length of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
Solution:Sum of two sides
= 12 cm + 15 cm = 27 cm
Difference of the two sides
= 15 cm – 12 cm = 3 cm
∴ The measure of third side should fall between 3 cm and 27 cm.
Exercise 6.5
1. PQR is a triangle, right angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
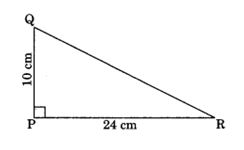
Solution:In right angled triangle PQR, we have
QR2 = PQ2 + PR2 From Pythagoras property)
= (10)2 + (24)2
= 100 + 576 = 676
∴ QR = √676 = 26 cm
The, the required length of QR = 26 cm.
2. ABC is a triangle, right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
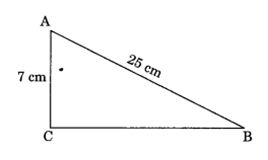
Solution:In right angled ∆ ABC, we have
BC2 + (7)2 = (25)2 (By Pythagoras property)
⇒ BC2 + 49 = 625
⇒ BC2 = 625 – 49
⇒ BC2 = 576
∴ BC = √576 = 24 cm
Thus, the required length of BC = 24 cm.
3. A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.
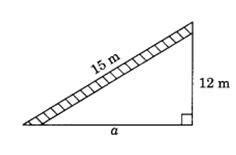
Solution:Here, the ladder forms a right angled triangle.
∴ a2 + (12)2 = (15)2 (By Pythagoras property)
⇒ a2+ 144 = 225
⇒ a2 = 225 – 144
⇒ a2 = 81
∴ a = √ 81 = 9 m
Thus, the distance of the foot from the ladder = 9m
4. Which of the following can be the sides of a right triangle?
(i) 2.5 cm, 6.5 cm, 6 cm.
(ii) 2 cm, 2 cm, 5 cm.
(iii) 1.5 cm, 2 cm, 2.5 cm
Solution:i) Given sides are 2.5 cm, 6.5 cm, 6 cm.
Square of the longer side = (6.5)2 = 42.25 cm.
Sum of the square of other two sides
= (2.5)2 + (6)2 = 6.25 + 36
= 42.25 cm.
Since, the square of the longer side in a triangle is equal to the sum of the squares of other two sides.
∴ The given sides form a right triangle.
(ii) Given sides are 2 cm, 2 cm, 5 cm .
Square of the longer side = (5)2 = 25 cm Sum of the square of other two sides
= (2)2 + (2)2 =4 + 4 = 8 cm
Since 25 cm ≠ 8 cm
∴ The given sides do not form a right triangle.
(iii) Given sides are 1.5 cm, 2 cm, 2.5 cm
Square of the longer side = (2.5)2 = 6.25 cm Sum of the square of other two sides
= (1.5)2 + (2)2 = 2.25 + 4
Since 6.25 cm = 6.25 cm = 6.25 cm
Since the square of longer side in a triangle is equal to the sum of square of other two sides.
∴ The given sides form a right triangle.
5. A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree . Find the original height of the tree.