Polynomials

• Polynomials
• Introduction
• Polynomials In One Variable
• Zeroes Of A Polynomial
• Remainder Theorem
• Factorisation Of Polynomials
• Algebraic Identities
• Summary

Polynomial is an algebraic expression that includes constants, variables, and exponents. It is the expression in which the variables have only positive integral.

Example

1. 4x³ + 3x² + x +3 is a polynomial in variable x.
2. 4x² + 3x^-1 – 4 is not a polynomial as it has negative power.
3. 3x^3/2 + 2x – 3 is not a polynomial.

• Polynomials are denoted by p(x), q(x) etc.
• In the above polynomial 2x², 3y and 2 are the terms of the polynomial.
• 2 and 3 are the coefficient of the x² and y respectively.
• x and y are the variables.
• 2 is the constant term which has no variable.

Polynomials in One Variable

If there is only one variable in the expression, then this is called the polynomial in one variable.

Example

• x³ + x – 4 is polynomial in variable x and is denoted by p(x).
• r² + 2 is polynomial in variable r and is denoted by p(r).

Types of polynomials on the basis of the number of terms

Number of non zero terms	Name	Example
0	Zero Polinomial	0
1	Monomial	X2
2	Binomial	X2+1
3	Trinomial	X3+1

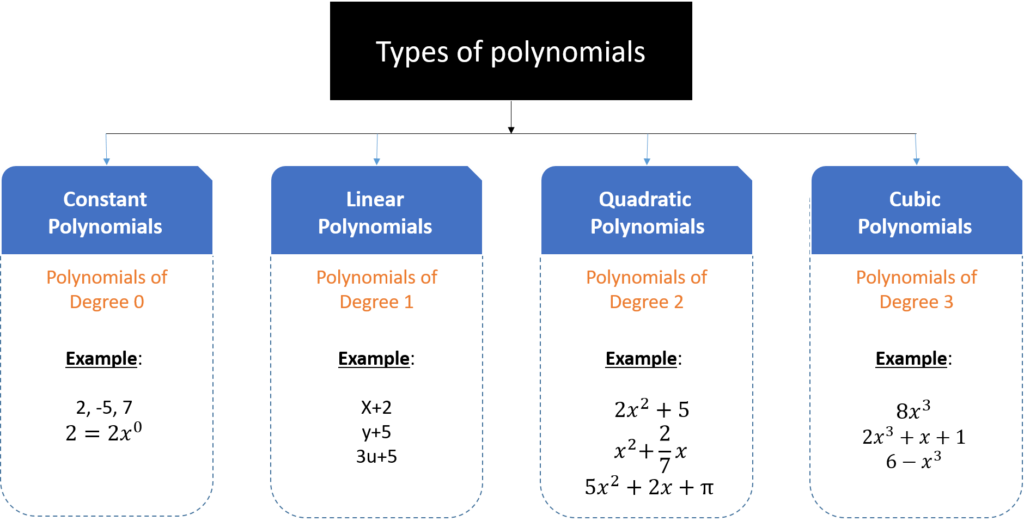
Types of polynomials on the basis of the number of degrees

The highest value of the power of the variable in the polynomial is the degree of the polynomial.

Zeroes of a Polynomial

If p(x) is a polynomial, then the number ‘a’ will be the zero of the polynomial with p(a) = 0. We can find the zero of the polynomial by equating it to zero.

Example: 1

Given polynomial is p(x) = x – 4

To find the zero of the polynomial we will equate it to zero.

x – 4 = 0

x = 4

p(4) = x – 4 = 4 – 4 = 0

This shows that if we place 4 in place of x, we got the value of the polynomial as zero. So 4 is the zero of this polynomial. And also we are getting the value 4 by equating the polynomial by 0.

So 4 is the zero of the polynomial or root of the polynomial.

The root of the polynomial is basically the x-intercept of the polynomial.

If the polynomial has one root, it will intersect the x-axis at one point only and, if it has two roots then it will intersect at two points and so on.

Example: 2

Find p (1) for the polynomial p (t) = t² – t + 1

p (1) = (1)² – 1 + 1

= 1 – 1 + 1

= 1

Example 2.1

Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer.

(i) 4x² – 3x + 7
(ii) y² + √2
(iii) 3 √t + t√2
(iv) y+ 2/y
(v) x¹⁰+ y³+t⁵⁰

Solution:
(i) We have 4x² – 3x + 7 = 4x² – 3x + 7x⁰
It is a polynomial in one variable i.e., x
because each exponent of x is a whole number.

(ii) We have y² + √2 = y² + √2y⁰
It is a polynomial in one variable i.e., y
because each exponent of y is a whole number.

(iii) We have 3 √t + t√2 = 3 √t^1/2 + √2.t
It is not a polynomial, because one of the exponents of t is 1/2,
which is not a whole number.

(iv) We have y + y+2/y = y + 2.y^-1
It is not a polynomial, because one of the exponents of y is -1,
which is not a whole number.

(v) We have x¹⁰+  y³ + t⁵⁰
Here, the exponent of every variable is a whole number, but x¹⁰ + y³ + t⁵⁰ is a polynomial in x, y, and t, i.e., in three variables.
So, it is not a polynomial in one variable.

2. Write the coefficients of x² in each of the following

(i) 2 + x² + x
(ii) 2 – x² + x³
(iii) π/2 x² + x
(iv) √2 x – 1

Solution:
(i) The given polynomial is 2 + x² + x.
The coefficient of x² is 1.
(ii) The given polynomial is 2 – x² + x³.
The coefficient of x² is -1.
(iii) The given polynomial is π/2 x 2 + x.
The coefficient of x² is π/2.
(iv) The given polynomial is √2 x – 1.
The coefficient of x² is 0.

3. Give one example each of a binomial of degree 35, and of a monomial of degree 100.

Solution:
(i) A binomial of degree 35 can be 3x³⁵ -4.
(ii) A monomial of degree 100 can be √2y¹⁰⁰.

4. Write the degree of each of the following polynomials.

(i) 5x³+4x² + 7x
(ii) 4 – y²
(iii) 5t – √7
(iv) 3

Solution:
(i) The given polynomial is 5x³ + 4x² + 7x.
The highest power of the variable x is 3.So, the degree of the polynomial is 3.

(ii) The given polynomial is 4- y². The highest power of the variable y is 2.
So, the degree of the polynomial is 2.

(iii) The given polynomial is 5t – √7 . The highest power of variable t is 1. So, the degree of the polynomial is 1.

(iv) Since, 3 = 3x° [∵ x°=1]
So, the degree of the polynomial is 0.

5. Classify the following as linear, quadratic and cubic polynomials.

(i) x²+ x
(ii) x – x³
(iii) y + y²+4
(iv) 1 + x
(v) 3t
(vi) r²
(vii) 7x³

Solution:
(i) The degree of x² + x is 2. So, it is a quadratic polynomial.
(ii) The degree of x – x³ is 3. So, it is a cubic polynomial.
(iii) The degree of y + y² + 4 is 2. So, it is a quadratic polynomial.
(iv) The degree of 1 + x is 1. So, it is a linear polynomial.
(v) The degree of 3t is 1. So, it is a linear polynomial.
(vi) The degree of r² is 2. So, it is a quadratic polynomial.
(vii) The degree of 7x³ is 3. So, it is a cubic polynomial.

Example 2.2

1. Find the value of the polynomial 5x – 4x² + 3 at
   (i) x = 0
   (ii) x = – 1
   (iii) x = 2

Solution:
1et p(x) = 5x – 4x² + 3
(i) p(0) = 5(0) – 4(0)² + 3

            = 0 – 0 + 3

             = 3
Thus, the value of 5x – 4x² + 3 at x = 0 is 3.

(ii) p(-1) = 5(-1) – 4(-1)² + 3
              = – 5x – 4x² + 3

              = -9 + 3

             = -6
Thus, the value of 5x – 4x² + 3 at x = -1 is -6.

(iii) p(2) = 5(2) – 4(2)² + 3

             = 10 – 4(4) + 3
             = 10 – 16 + 3

             = -3
Thus, the value of 5x – 4x² + 3 at x = 2 is – 3.

2. Find p (0), p (1) and p (2) for each of the following polynomials.
(i) p(y) = y² – y +1
(ii) p (t) = 2 +1 + 2t² -t³
(iii) P (x) = x³
(iv) p (x) = (x-1) (x+1)

Solution:
(i) Given that p(y) = y² – y + 1.
∴ P(0) = (0)² – 0 + 1 = 0 – 0 + 1 = 1
p(1) = (1)² – 1 + 1 = 1 – 1 + 1 = 1
p(2) = (2)² – 2 + 1 = 4 – 2 + 1 = 3

(ii) Given that p(t) = 2 + t + 2t² – t³
∴p(0) = 2 + 0 + 2(0)² – (0)³
= 2 + 0 + 0 – 0=2
P(1) = 2 + 1 + 2(1)² – (1)³
= 2 + 1 + 2 – 1 = 4
p( 2) = 2 + 2 + 2(2)² – (2)³
= 2 + 2 + 8 – 8 = 4

(iii) Given that p(x) = x³
∴ p(0) = (0)³ = 0, p(1) = (1)³ = 1
p(2) = (2)³ = 8

(iv) Given that p(x) = (x – 1)(x + 1)
∴ p(0) = (0 – 1)(0 + 1) = (-1)(1) = -1
p(1) = (1 – 1)(1 +1) = (0)(2) = 0
P(2) = (2 – 1)(2 + 1) = (1)(3) = 3

3. Verify whether the following are zeroes of the polynomial, indicated against them.
(i) p(x) = 3x + 1,x = –1/3
(ii) p (x) = 5x – π, x = 4/5
(iii) p (x) = x² – 1, x = x – 1
(iv) p (x) = (x + 1) (x – 2), x = – 1,2
(v) p (x) = x², x = 0
(vi) p (x) = 1x + m, x = – m/1
(vii) P (x) = 3x² – 1, x = – 1/√3,2/√3
(viii) p (x) = 2x + 1, x = ½

Solution:
(i) We have , p(x) = 3x + 1

(ii) We have, p(x) = 5x – π
∴ p(−1/3)=3(−1/3)+1=−1+1=0

(iii) We have, p(x) = x² – 1
∴ p(1) = (1)² – 1 = 1 – 1=0
Since, p(1) = 0, so x = 1 is a zero of x² -1.
Also, p(-1) = (-1)² -1 = 1 – 1 = 0
Since p(-1) = 0, so, x = -1, is also a zero of x² – 1.

(iv) We have, p(x) = (x + 1)(x – 2)
∴ p(-1) = (-1 +1) (-1 – 2) = (0)(- 3) = 0
Since, p(-1) = 0, so, x = -1 is a zero of (x + 1)(x – 2).
Also, p( 2) = (2 + 1)(2 – 2) = (3)(0) = 0
Since, p(2) = 0, so, x = 2 is also a zero of (x + 1)(x – 2).

(v) We have, p(x) = x²
∴ p(o) = (0)² = 0
Since, p(0) = 0, so, x = 0 is a zero of x². (vi) We have, p(x) = lx + m

(vii) We have, p(x) = 3x² – 1

(viii) We have, p(x) = 2x + 1
∴ p(1/2)=2(1/2)+1=1+1=2
Since, p(1/2) ≠ 0, so, x = 12 is not a zero of 2x + 1.

4. Find the zero of the polynomial in each of the following cases
(i) p(x)=x+5
(ii) p (x) = x – 5
(iii) p (x) = 2x + 5
(iv) p (x) = 3x – 2
(v) p (x) = 3x
(vi) p (x)= ax, a≠0
(vii) p (x) = cx + d, c ≠ 0 where c and d are real numbers.

Solution:
(i) We have, p(x) = x + 5. Since, p(x) = 0
⇒ x + 5 = 0
⇒ x = -5.
Thus, zero of x + 5 is -5.

(ii) We have, p(x) = x – 5.
Since, p(x) = 0 ⇒ x – 5 = 0 ⇒ x = -5
Thus, zero of x – 5 is 5.

(iii) We have, p(x) = 2x + 5. Since, p(x) = 0
⇒ 2x + 5 =0
⇒ 2x = -5
⇒ x = −5/2
Thus, zero of 2x + 5 is −5/2 .

(iv) We have, p(x) = 3x – 2. Since, p(x) = 0
⇒ 3x – 2 = 0
⇒ 3x = 2
⇒ x = 2/3
Thus, zero of 3x – 2 is 2/3

(v) We have, p(x) = 3x. Since, p(x) = 0
⇒ 3x = 0 ⇒ x = 0
Thus, zero of 3x is 0.

(vi) We have, p(x) = ax, a ≠ 0.
Since, p(x) = 0 => ax = 0 => x-0
Thus, zero of ax is 0.

(vii) We have, p(x) = cx + d. Since, p(x) = 0
⇒ cx + d = 0 ⇒ cx = -d ⇒ x=−d/c
Thus, zero of cx + d is –d/c

Example 2.3

Find the remainder when x³ + 3x² + 3x + 1 is divided by
(i) x + 1
(ii) x – 1/2
(iii) x
(iv) x + π
(v) 5 + 2x

Solution:
Let p(x) = x³ + 3x² + 3x +1
(i) The zero of x + 1 is -1.
∴ p(-1) = (-1)3 + 3(-1)2 + 3(-1) +1
= -1 + 3- 3 + 1 = 0
Thus, the required remainder = 0

(ii) The zero of x−12 is 12

Thus, the required remainder = 27/8

(iii) The zero of x is 0.
∴ p(0) = (0)³ + 3(0)² + 3(0) + 1
= 0 + 0 + 0 + 1 = 1
Thus, the required remainder = 1.

(iv) The zero of x + π is -π.
p(-π) = (-π)³ + 3(- π)²2 + 3(- π) +1
= -π³ + 3π² + (-3π) + 1
= – π³ + 3π² – 3π +1
Thus, the required remainder is -π³ + 3π² – 3π+1.

(v) The zero of 5 + 2x is −5/2 .

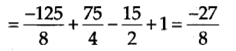
Thus, the required remainder is −27/8 .

2. Find the remainder when x³ – ax² + 6x – a is divided by x – a.

Solution:
We have, p(x) = x³ – ax² + 6x – a and zero of x – a is a.
∴ p(a) = (a)³ – a(a)² + 6(a) – a
= a³ – a³ + 6a – a = 5a
Thus, the required remainder is 5a. 3. Check whether 7 + 3x is a factor of 3x³+7x.
Solution:
We have, p(x) = 3x³+7x. and zero of 7 + 3x is −7/3.

Since,( −490/9) ≠ 0
i.e. the remainder is not 0.
∴ 3x³ + 7x is not divisib1e by 7 + 3x.
Thus, 7 + 3x is not a factor of 3x³ + 7x.

Example 2.4

1. Determine which of the following polynomials has (x +1) a factor.
   (i) x³+x²+x +1
   (ii) x⁴ + x³ + x² + x + 1
   (iii) x⁴ + 3x³ + 3x² + x + 1
   (iv) x³ – x² – (2 +√2 )x + √2

Solution:
The zero of x + 1 is -1.
(i) Let p (x) = x³ + x² + x + 1
∴ p (-1) = (-1)³ + (-1)² + (-1) + 1 .
= -1 + 1 – 1 + 1
⇒ p (- 1) = 0
So, (x+ 1) is a factor of x³ + x² + x + 1.

(ii) Let p (x) = x⁴ + x³ + x² + x + 1
∴ P(-1) = (-1)⁴ + (-1)³ + (-1)² + (-1)+1
= 1 – 1 + 1 – 1 + 1
⇒ P (-1) ≠ 1
So, (x + 1) is not a factor of x⁴ + x³ + x² + x+ 1

(iii) Let p (x) = x⁴ + 3x³ + 3x² + x + 1 .
∴ p (-1)= (-1)⁴ + 3 (-1)³ + 3 (-1)² + (- 1) + 1
= 1 – 3 + 3 – 1 + 1 = 1
⇒ p (-1) ≠ 0
So, (x + 1) is not a factor of x⁴ + 3x³ + 3x² + x+ 1.

(iv) Let p (x) = x³ – x² – (2 + √2) x + √2
∴ p (- 1) =(- 1)3- (-1)2 – (2 + √2)(-1) + √2
= -1 – 1 + 2 + √2 + √2
= 2√2
⇒ p (-1) ≠ 0
So, (x + 1) is not a factor of x³ – x² – (2 + √2) x + √2.

2. Use the Factor Theorem to determine whether g (x) is a factor of p (x) in each of the following cases

(i) p (x)= 2x³ + x² – 2x – 1, g (x) = x + 1
(ii) p(x)= x³ + 3x² + 3x + 1, g (x) = x + 2
(iii) p (x) = x³ – 4x² + x + 6, g (x) = x – 3

Solution:
(i) We have, p (x)= 2x³ + x² – 2x – 1 and g (x) = x + 1
∴ p(-1) = 2(-1)³ + (-1)² – 2(-1) – 1
= 2(-1) + 1 + 2 – 1
= -2 + 1 + 2 -1 = 0
⇒ p(-1) = 0, so g(x) is a factor of p(x).

(ii) We have, p(x) x³ + 3x² + 3x + 1 and g(x) = x + 2
∴ p(-2) = (-2)³ + 3(-2)²+ 3(-2) + 1
= -8 + 12 – 6 + 1
= -14 + 13
= -1
⇒ p(-2) ≠ 0, so g(x) is not a factor of p(x).

(iii) We have, = x³ – 4x² + x + 6 and g (x) = x – 3
∴ p(3) = (3)³ – 4(3)² + 3 + 6
= 27 – 4(9) + 3 + 6
= 27 – 36 + 3 + 6 = 0
⇒ p(3) = 0, so g(x) is a factor of p(x).

3. Find the value of k, if x – 1 is a factor of p (x) in each of the following cases

(i) p (x) = x² + x + k
(ii) p (x) = 2x² + kx + √2
(iii) p (x) = kx² – √2 x + 1
(iv) p (x) = kx² – 3x + k

Solution:
For (x – 1) to be a factor of p(x), p(1) should be equal to 0.

(i) Here, p(x) = x² + x + k
Since, p(1) = (1)² +1 + k
⇒ p(1) = k + 2 = 0
⇒ k = -2.

(ii) Here, p (x) = 2x² + kx + √2
Since, p(1) = 2(1)² + k(1) + √2
= 2 + k + √2 =0
k = -2 – √2 = -(2 + √2)

(iii) Here, p (x) = kx² – √2 x + 1
Since, p(1) = k(1)² – (1) + 1
= k – √2 + 1 = 0
⇒ k = √2 -1

(iv) Here, p(x) = kx² – 3x + k
p(1) = k(1)² – 3(1) + k
= k – 3 + k
= 2k – 3 = 0
⇒ k = ¾

4. Factorise

(i) 12x² – 7x +1
(ii) 2x² + 7x + 3
(iii) 6x² + 5x – 6
(iv) 3x² – x – 4

Solution:
(i) We have,
12x² – 7x + 1 = 12x² – 4x- 3x + 1
= 4x (3x – 1 ) -1 (3x – 1)
= (3x -1) (4x -1)
Thus, 12x² -7x + 3 = (2x – 1) (x + 3)

(ii) We have, 2x² + 7x + 3 = 2x² + x + 6x + 3
= x(2x + 1) + 3(2x + 1)
= (2x + 1)(x + 3)
Thus, 2×2 + 7x + 3 = (2x + 1)(x + 3)

(iii) We have, 6x² + 5x – 6 = 6x² + 9x – 4x – 6
= 3x(2x + 3) – 2(2x + 3)
= (2x + 3)(3x – 2)
Thus, 6x² + 5x – 6 = (2x + 3)(3x – 2)

(iv) We have, 3x² – x – 4 = 3x² – 4x + 3x – 4
= x(3x – 4) + 1(3x – 4) = (3x – 4)(x + 1)
Thus, 3x² – x – 4 = (3x – 4)(x + 1)

5. Factorise

(i) x³ – 2x² – x + 2
(ii) x³ – 3x² – 9x – 5
(iii) x³ + 13x² + 32x + 20
(iv) 2y³ + y² – 2y – 1

Solution:
(i) We have, x³ – 2x² – x + 2
Rearranging the terms, we have x³ – x – 2x² + 2
= x(x² – 1) – 2(x² -1) = (x² – 1)(x – 2)
= [(x)² – (1)²](x – 2)
= (x – 1)(x + 1)(x – 2)
[∵ (a² – b²) = (a + b)(a-b)]
Thus, x³ – 2x² – x + 2 = (x – 1)(x + 1)(x – 2)

(ii) We have, x³ – 3x² – 9x – 5
= x³ + x² – 4x² – 4x – 5x – 5 ,
= x² (x + 1) – 4x(x + 1) – 5(x + 1)
= (x + 1)(x² – 4x – 5)
= (x + 1)(x² – 5x + x – 5)
= (x + 1)[x(x – 5) + 1(x – 5)]
= (x + 1)(x – 5)(x + 1)
Thus, x³ – 3x² – 9x – 5 = (x + 1)(x – 5)(x +1)

(iii) We have, x³ + 13x² + 32x + 20
= x³ + x² + 12x² + 12x + 20x + 20
= x²(x + 1) + 12x(x +1) + 20(x + 1)
= (x + 1)(x² + 12x + 20)
= (x + 1)(x² + 2x + 10x + 20)
= (x + 1)[x(x + 2) + 10(x + 2)]
= (x + 1)(x + 2)(x + 10)
Thus, x³ + 13x² + 32x + 20
= (x + 1)(x + 2)(x + 10)

(iv) We have, 2y³ + y² – 2y – 1
= 2y³ – 2y² + 3y² – 3y + y – 1
= 2y²(y – 1) + 3y(y – 1) + 1(y – 1)
= (y – 1)(2y² + 3y + 1)
= (y – 1)(2y² + 2y + y + 1)
= (y – 1)[2y(y + 1) + 1(y + 1)]
= (y – 1)(y + 1)(2y + 1)
Thus, 2y³ + y² – 2y – 1
= (y – 1)(y + 1)(2y +1)

Example 2.5

1. Use suitable identities to find the following products
   (i) (x + 4)(x + 10)
   (ii) (x+8) (x -10)
   (iii) (3x + 4) (3x – 5)
   (iv) (y²+ 3/2) (y²– 3/2)
   (v) (3 – 2x) (3 + 2x)

Solution:
(i) We have, (x+ 4) (x + 10)
Using identity,
(x+ a) (x+ b) = x² + (a + b) x+ ab.
We have, (x + 4) (x + 10) = x²+(4 + 10) x + (4 x 10)
= x² + 14x+40

(ii) We have, (x+ 8) (x -10)
Using identity,
(x + a) (x + b) = x² + (a + b) x + ab
We have, (x + 8) (x – 10) = x² + [8 + (-10)] x + (8) (- 10)
= x² – 2x – 80

(iii) We have, (3x + 4) (3x – 5)
Using identity,
(x + a) (x + b) = x² + (a + b) x + ab
We have, (3x + 4) (3x – 5) = (3x)² + (4 – 5) x + (4) (- 5)
= 9x² – x – 20

2. Evaluate the following products without multiplying directly
(i) 103 x 107
(ii) 95 x 96
(iii) 104 x 96

Solution:
(i)We have, 103 x 107 = (100 + 3) (100 + 7)
= ( 100)² + (3 + 7) (100)+ (3 x 7)
[Using (x + a)(x + b) = x² + (a + b)x + ab]
= 10000 + (10) x 100 + 21
= 10000 + 1000 + 21=11021

(ii) We have, 95 x 96 = (100 – 5) (100 – 4)
= ( 100)² + [(- 5) + (- 4)] 100 + (- 5 x – 4)
[Using (x + a)(x + b) = x² + (a + b)x + ab]
= 10000 + (-9) + 20 = 9120
= 10000 + (-900) + 20 = 9120

(iii) We have 104 x 96 = (100 + 4) (100 – 4)
= (100)²-4²
[Using (a + b)(a -b) = a²– b²]
= 10000 – 16 = 9984

3. Factorise the following using appropriate identities
(i) 9x² + 6xy + y²
(ii) 4y²-4y + 1
(iii) x² – y2/100

Solution:
(i) We have, 9x² + 6xy + y²
= (3x)² + 2(3x)(y) + (y)²
= (3x + y)²
[Using a² + 2ab + b² = (a + b)²]
= (3x + y)(3x + y)

(ii) We have, 4y² – 4y + 1²
= (2y)² + 2(2y)(1) + (1)²
= (2y -1)²
[Using a² – 2ab + b² = (a- b)²]
= (2y – 1)(2y – 1 )

4. Expand each of the following, using suitable identity
(i) (x+2y+ 4z)²
(ii) (2x – y + z)²
(iii) (- 2x + 3y + 2z)²
(iv) (3a -7b – c)^z
(v) (- 2x + 5y – 3z)²
(vi) [ 1/4a –1/4b + 1] ²

Solution:
We know that
(x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx

(i) (x + 2y + 4z)²
= x² + (2y)² + (4z)² + 2 (x) (2y) + 2 (2y) (4z) + 2(4z) (x)
= x² + 4y² + 16z² + 4xy + 16yz + 8 zx

(ii) (2x – y + z)² = (2x)² + (- y)² + z² + 2 (2x) (- y)+ 2 (- y) (z) + 2 (z) (2x)
= 4x² + y² + z² – 4xy – 2yz + 4zx

(iii) (- 2x + 3y + 2z)² = (- 2x)² + (3y)² + (2z)² + 2 (- 2x) (3y)+ 2 (3y) (2z) + 2 (2z) (- 2x)
= 4x² + 9y² + 4z² – 12xy + 12yz – 8zx

(iv) (3a -7b- c)² = (3a)² + (- 7b)² + (- c)² + 2 (3a) (- 7b) + 2 (- 7b) (- c) + 2 (- c) (3a)
= 9a² + 49b² + c² – 42ab + 14bc – 6ac

(v)(- 2x + 5y- 3z)² = (- 2x)² + (5y)² + (- 3z)² + 2 (- 2x) (5y) + 2 (5y) (- 3z) + 2 (- 3z) (- 2x)
= 4x² + 25y² + 9z² – 20xy – 30yz + 12zx

5. Factorise
(i) 4 x² + 9y² + 16z² + 12xy – 24yz – 16xz
(ii) 2x² + y² + 8z² – 2√2xy + 4√2yz – 8xz

Solution:
(i) 4x² + 9y² + 16z² + 12xy – 24yz – 16xz
= (2x)² + (3y)² + (- 4z)² + 2 (2x) (3y) + 2 (3y) (- 4z) + 2 (- 4z) (2x)
= (2x + 3y – 4z)² = (2x + 3y + 4z) (2x + 3y – 4z)

(ii) 2x² + y² + 8z² – 2√2xy + 4√2yz – 8xz
= (- √2x)² + (y)² + (2 √2z)²y + 2(- √2x) (y)+ 2 (y) (2√2z) + 2 (2√2z) (- √2x)
= (- √2x + y + 2 √2z)²
= (- √2x + y + 2 √2z) (- √2x + y + 2 √2z)

6. Write the following cubes in expanded form

Solution:
We have, (x + y)³ = x³ + y³ + 3xy(x + y) …(1)
and (x – y)³ = x³ – y³ – 3xy(x – y) …(2)

(i) (2x + 1)³ = (2x)³ + (1)³ + 3(2x)(1)(2x + 1) [By (1)]
= 8x³ + 1 + 6x(2x + 1)
= 8x³ + 12x² + 6x + 1

(ii) (2a – 3b)³ = (2a)³ – (3b)³ – 3(2a)(3b)(2a – 3b) [By (2)]
= 8a³ – 27b³ – 18ab(2a – 3b)
= 8a³ – 27b³ – 36a²b + 54ab²

7. Evaluate the following using suitable identities

(i) (99)³
(ii) (102)³
(iii) (998)³

Solution:
(i) We have, 99 = (100 -1)
∴ 99³ = (100 – 1)³
= (100)³ – 1³ – 3(100)(1)(100 -1)
[Using (a – b)³ = a³ – b³ – 3ab (a – b)]
= 1000000 – 1 – 300(100 – 1)
= 1000000 -1 – 30000 + 300
= 1000300 – 30001 = 970299

(ii) We have, 102 =100 + 2
∴ 102³ = (100 + 2)³
= (100)³ + (2)³ + 3(100)(2)(100 + 2)
[Using (a + b)³ = a³ + b³ + 3ab (a + b)]
= 1000000 + 8 + 600(100 + 2)
= 1000000 + 8 + 60000 + 1200 = 1061208

(iii) We have, 998 = 1000 – 2
∴ (998)³ = (1000-2)³
= (1000)³– (2)³ – 3(1000)(2)(1000 – 2)
[Using (a – b)³ = a³ – b³ – 3ab (a – b)]
= 1000000000 – 8 – 6000(1000 – 2)
= 1000000000 – 8 – 6000000 +12000
= 994011992

8.Factorise each of the following
(i) 8a³ +b³ + 12a²b+6ab²
(ii) 8a³ -b³-12a²b+6ab²
(iii) 27-125a³ -135a+225a²
(iv) 64a³ -27b³ -144a²b + 108ab²

Solution:
(i) 8a³ +b³ +12a²b+6ab²
= (2a)³ + (b)³ + 6ab(2a + b)
= (2a)³ + (b)³ + 3(2a)(b)(2a + b)
= (2 a + b)³
[Using a³ + b³ + 3 ab(a + b) = (a + b)³]
= (2a + b)(2a + b)(2a + b)

(ii) 8a³ – b³ – 12o²b + 6ab²
= (2a)³ – (b)³ – 3(2a)(b)(2a – b)
= (2a – b)³
[Using a³ + b³ + 3 ab(a + b) = (a + b)³]
= (2a – b) (2a – b) (2a – b)

(iii) 27 – 125a³ – 135a + 225a²
= (3)³ – (5a)³ – 3(3)(5a)(3 – 5a)
= (3 – 5a)³
[Using a³ + b³ + 3 ab(a + b) = (a + b)³]
= (3 – 5a) (3 – 5a) (3 – 5a)

(iv) 64a³ -27b³ -144a²b + 108ab²
= (4a)³ – (3b)³ – 3(4a)(3b)(4a – 3b)
= (4a – 3b)³
[Using a³ – b³ – 3 ab(a – b) = (a – b)³]
= (4a – 3b)(4a – 3b)(4a – 3b)

9. Verify
(i) x³ + y³ = (x + y)-(x² – xy + y²)
(ii) x³ – y³ = (x – y) (x² + xy + y²)

Solution:
(i) ∵ (x + y)³ = x³ + y³ + 3xy(x + y)
⇒ (x + y)³ – 3(x + y)(xy) = x³ + y³
⇒ (x + y)[(x + y)2-3xy] = x³ + y³
⇒ (x + y)(x² + y² – xy) = x³ + y³
Hence, verified.

(ii) ∵ (x – y)³ = x³ – y³ – 3xy(x – y)
⇒ (x – y)³ + 3xy(x – y) = x³ – y³
⇒ (x – y)[(x – y)² + 3xy)] = x³ – y³
⇒ (x – y)(x² + y² + xy) = x³ – y³
Hence, verified.

10.Factorise each of the following
(i) 27y³ + 125z³
(ii) 64m³ – 343n³
[Hint See question 9]

Solution:
(i) We know that
x³ + y³ = (x + y)(x² – xy + y²)
We have, 27y³ + 125z³ = (3y)³ + (5z)³
= (3y + 5z)[(3y)² – (3y)(5z) + (5z)²]
= (3y + 5z)(9y² – 15yz + 25z²)

(ii) We know that
x³ – y³ = (x – y)(x² + xy + y²)
We have, 64m³ – 343n³ = (4m)³ – (7n)³
= (4m – 7n)[(4m)² + (4m)(7n) + (7n)²]
= (4m – 7n)(16m² + 28mn + 49n²)

10.Factorise each of the following
(i) 27y³ + 125z³
(ii) 64m³ – 343n³
[Hint See question 9]

Solution:
(i) We know that
x³ + y³ = (x + y)(x² – xy + y²)
We have, 27y³ + 125z³ = (3y)³ + (5z)³
= (3y + 5z)[(3y)² – (3y)(5z) + (5z)²]
= (3y + 5z)(9y² – 15yz + 25z²)

(ii) We know that
x³ – y³ = (x – y)(x² + xy + y²)
We have, 64m³ – 343n³ = (4m)³ – (7n)³
= (4m – 7n)[(4m)² + (4m)(7n) + (7n)²]
= (4m – 7n)(16m² + 28mn + 49n²)

11.Factorise 27x³ +y³ +z³ -9xyz

Solution:
We have,
27x³ + y³ + z³ – 9xyz = (3x)³ + (y)³ + (z)³ – 3(3x)(y)(z)
Using the identity,
x³ + y³ + z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx)
We have, (3x)³ + (y)³ + (z)³ – 3(3x)(y)(z)
= (3x + y + z)[(3x)³ + y³ + z³ – (3x × y) – (y × 2) – (z × 3x)]
= (3x + y + z)(9x² + y² + z² – 3xy – yz – 3zx)

12.Verify that
x³ +y³ +z³ – 3xyz = 1/2 (x + y+z)[(x-y)² + (y – z)² +(z – x)²]

Solution:
R.H.S
= 1/2(x + y + z)[(x – y)²+(y – z)²+(z – x)²]
= 1/2 (x + y + 2)[(x² + y² – 2xy) + (y² + z² – 2yz) + (z² + x² – 2zx)]
= 1/2 (x + y + 2)(x² + y² + y² + z² + z² + x² – 2xy – 2yz – 2zx)
= 1/2 (x + y + z)[2(x² + y² + z² – xy – yz – zx)]
= 2 x 1/2 x (x + y + z)(x² + y² + z² – xy – yz – zx)
= (x + y + z)(x² + y² + z² – xy – yz – zx)
= x³ + y³ + z³ – 3xyz = L.H.S.
Hence, verified.

13. If x + y + z = 0, show that x³ + y³ + z³ = 3 xyz.

Solution:
Since, x + y + z = 0
⇒ x + y = -z (x + y)³ = (-z)³
⇒ x³ + y³ + 3xy(x + y) = -z³
⇒ x³ + y³ + 3xy(-z) = -z³ [∵ x + y = -z]
⇒ x³ + y³ – 3xyz = -z³
⇒ x³ + y³ + z³ = 3xyz
Hence, if x + y + z = 0, then
x³ + y³ + z³ = 3xyz

14. Without actually calculating the cubes, find the value of each of the following
(i) (- 12)³ + (7)³ + (5)³
(ii) (28)³ + (- 15)³ + (- 13)³
Solution:
(i) We have, (-12)³ + (7)³ + (5)³
Let x = -12, y = 7 and z = 5.
Then, x + y + z = -12 + 7 + 5 = 0
We know that if x + y + z = 0, then, x³ + y³ + z³ = 3xyz
∴ (-12)³ + (7)³ + (5)³ = 3[(-12)(7)(5)]
= 3[-420] = -1260

(ii) We have, (28)³ + (-15)³ + (-13)³
Let x = 28, y = -15 and z = -13.
Then, x + y + z = 28 – 15 – 13 = 0
We know that if x + y + z = 0, then x³ + y³ + z³ = 3xyz
∴ (28)³ + (-15)³ + (-13)³ = 3(28)(-15)(-13)
= 3(5460) = 16380

15. Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given
(i) Area 25a² – 35a + 12
(ii) Area 35y² + 13y – 12
Solution:
Area of a rectangle = (Length) x (Breadth)
(i) 25a² – 35a + 12 = 25a² – 20a – 15a + 12 = 5a(5a – 4) – 3(5a – 4) = (5a – 4)(5a – 3)
Thus, the possible length and breadth are (5a – 3) and (5a – 4).

(ii) 35y²+ 13y -12 = 35y² + 28y – 15y -12
= 7y(5y + 4) – 3(5y + 4) = (5 y + 4)(7y – 3)
Thus, the possible length and breadth are (7y – 3) and (5y + 4).

16. What are the possible expressions for the dimensions of the cuboids whose volumes are given below?
(i) Volume 3x² – 12x
(ii) Volume 12ky² + 8ky – 20k

Solution:
Volume of a cuboid = (Length) x (Breadth) x (Height)
(i) We have, 3x² – 12x = 3(x² – 4x)
= 3 x x x (x – 4)
∴ The possible dimensions of the cuboid are 3, x and (x – 4).

(ii) We have, 12ky² + 8ky – 20k
= 4[3ky² + 2ky – 5k] = 4[k(3y² + 2y – 5)]
= 4 x k x (3y² + 2y – 5)
= 4k[3y² – 3y + 5y – 5]
= 4k[3y(y – 1) + 5(y – 1)]
= 4k[(3y + 5) x (y – 1)]
= 4k x (3y + 5) x (y – 1)
Thus, the possible dimensions of the cuboid are 4k, (3y + 5) and (y -1).