TRIANGLES

Similarity of Triangles

In the Triangles also we will use the same condition that the two Triangles will be similar if-

• The corresponding angles of the two Triangles are same and
• The corresponding sides of the two Triangles are in same proportion.

The above two Triangles ∆ABC and ∆DEF are similar as-

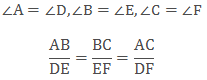
If the corresponding angles of the two Triangles are same then they are called equiangular Triangle

Basic Proportionality Theorem (Thales Theorem)

According to Thales theorem, if in a given Triangle a line is drawn parallel to any of the sides of the Triangle so that the other two sides intersect at some distinct point then it divides the two sides in the same ratio

In ∆KMN, if PQ║MN and intersects KM at P and KN at Q, then,

1)KP   =     KO

PM         QN

2)KM =     KN

KP           KQ

3)KM =KN

PM QN

Converse of Basic Proportionality Theorem

It is the opposite of basic proportionality theorem, which says that if in a given Triangle a straight line divides the two sides of the Triangle in the same ratio then that straight line is parallel to the third side of the Triangle.

Criteria for the similarity of Triangles

Basically, there are three criteria to find the similarity of two Triangles.

1. AAA(angle-Angle-Angle) criteria of similarity

If in two given Triangles all the corresponding angles are equal then their corresponding sides will also be in proportion.

This shows that all the corresponding angles in the ∆ABC and ∆PQR are same so their corresponding sides are in proportion, that why the two Triangles similar.

Hence, ∆ABC ~ ∆PQR

Remark: If the two corresponding angles of the two Triangles are equal then according to the sum of angles of Triangle, the third angle will also be equal. So two Triangles will be similar if their two angles are equal with the two angles of another Triangle.This is known as AA (Angle-Angle) criteria.

2. SSS(Side-Side-Side) criteria of similarity

If in the two Triangles, all the sides of one Triangle are in same ratio with the corresponding sides of the other Triangle, then their corresponding angles will be equal. Hence the two Triangles are similar.

In ∆ABC and ∆DEF

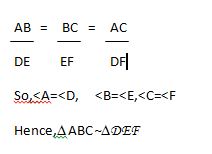
Remark: The above two criterion shows that if any of the two criteria satisfies then the other implies itself. So we need not check for both the conditions to satisfy to find the similarity of the two Triangles. If all the angles are equal then all the sides will be in proportion itself and vice versa.

3. SAS(Side-Angle-Side)criteria of similarity

If in the two Triangles, two sides are in the same ratio with the two sides of the other Triangle and the angle including those sides is equal then these two Triangles will be similar.

In ∆ABC and ∆KLM

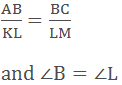
Hence, ∆ABC ~ ∆KLM

Areas of similar Triangles

If the two similar Triangles are given then the square of the ratio of their corresponding sides will be equal to the ratio of their area.

If ∆ABC ~ ∆PQR, then

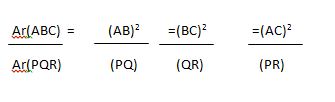
Pythagoras Theorem (Baudhayan Theorem)

Pythagoras theorem says that in a right angle Triangle, the square of the hypotenuse i.e. the side opposite to the right angle is equal to the sum of the square of the other two sides of the Triangle.

If one angle is 90°, then a² + b² = c²

Converse of Pythagoras Theorem

In a Triangle, if the sum of the square of the two sides is equal to the square of the third side then the given Triangle is a right angle Triangle.

If a² + b² = c² then one angle is 90°.

Similarity of two Triangles made in right angle Triangle

In a right angle Triangle, if we draw a perpendicular from the right angle to the hypotenuse of the Triangle, then both the new Triangles will be similar to the whole Triangle.

In the above right angle Triangle CP is the vertex on the hypotenuse, so

∆ACP ~ ∆ACB

∆PCB ~ ∆ACB

∆PCB ~ ∆ACP

Exercise 2.1

1. Fill in the blanks by using the correct word given in brackets.
(i) All circles are ……………. . (congruent/similar)
(ii) All squares are …………… . (similar/congruent)
(iii) All …………….. triangles are similar. (isosceles/equilateral)
(iv) Two polygons of the same number of sides are similar, if
(a) their corresponding angles are …………… and
(b) their corresponding sides are …………… (equal/proportional)
Solution:

2. Give two different examples of pairs of
(i) similar figures.
(ii) non-similar figures.
Solution:

i)Similar figures

A pair of equilaterial triangles of different side lengths, a pair of two rectangles of different lengths and breadths. etc.

ii)Non-similar figures

A pair of rectangle and a parallelogram with angles not equal to 90⁰ a pair of an isoscles triangles and a scalene triangle etc.

3. State whether the following quadrilaterals are similar or not.

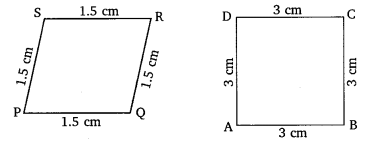
Solution:

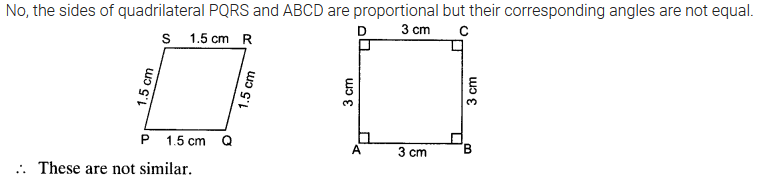
THALES THEOREM

STATEMENT: If a line is drawn parallel to one side of a triangle it intersect the other two sides in different points the other two sides are divided in the same ratio.’

Given:In  ∆ABC , DE ǁ BC

To Prove:

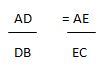
Construction: Join B , E  and D, C Draw DM ⊥ AC  and EN ⊥ AB

In the given figure (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).

2. E and F are points on the sides PQ and PR respectively of a ∆PQR. For each of the following cases, state whether EF || QR:
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm

(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm

(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Solution:

3.In the given figure, if LM || CB and LN || CD. Prove that AM/AB=AN/AD∙

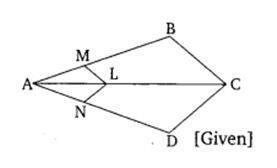
 6. In the given figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

7. Using B.P.T., prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that your have proved it in class IX)

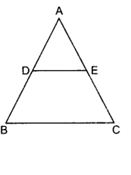
8. Using converse of B.P.T., prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side.  (Recall that your have done it in class IX)

Solution:

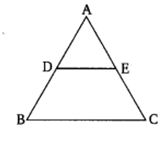
The given figures show ABC in which D and E are mid-point of sides AB and AC res.

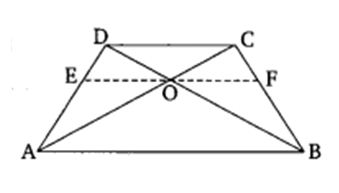
9. ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that AO/BO=CO/DO∙
Solution:

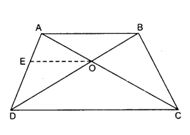
10.The diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO=CODO∙ Show that ABCD is a trapezium.

Solution:In the given figure is shown a quadrilateral ABCD. Draw EF║AB

Two triangles are similar if either of the following three criterion’s are satisfied:

1.AAA similarity Criterion. If two triangles are equiangular, then they are similar.

2.Corollary(AA similarity). If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.

3.SSS Similarity Criterion. If the corresponding sides of two triangles are proportional, then they are similar.

4. SAS Similarity Criterion. If in two triangles, one pair of corresponding sides are proportional and the included angles are equal, then the two triangles are similar.

Results in Similar Triangles based on Similarity Criterion:

1.Ratio of corresponding sides = Ratio of corresponding perimeters

2.Ratio of corresponding sides = Ratio of corresponding medians

3.Ratio of corresponding sides = Ratio of corresponding altitudes

4.Ratio of corresponding sides = Ratio of corresponding angle bisector segments.

THEOREM: If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar. This is also called AAA (Angle-Angle-Angle) criterion.

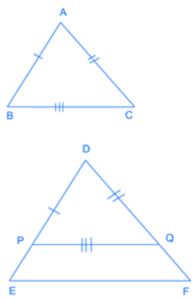
Given: In ΔABC and ΔPQR, ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R.

Construction: Two triangles ABC and DEF are drawn so that their corresponding angles are equal. This means:

∠ A =∠ D, ∠ B = ∠ E and ∠ C = ∠ F

To prove:

AB/DE=AC/DF=BC/EF

Draw a line PQ in the second triangle so that DP = AB and PQ = AC

Proof:

ΔABC≅ΔDPQΔABC≅ΔDPQ

Because corresponding sides of these two triangles are equal

This means; ∠ B = ∠ P = ∠ E and PQ || EF

∠ P =∠ E, ∠ Q = ∠ F [CORRESPONDING ANGLES]