Summary of lines and angles

Solved exercise of lines and angles

Summary

This chapter tells you to find out the properties of angel formed when two lines intersect each other and also angles formed when two or more line intersect at distinct point.

Uses of Lines and angels

Suppose you want to build a hut to keep it in your school exhibition using a bamboo sticks. We should keep some sticks  parallel to each other and some slanted  so with the help of these angles and lines we can do this.

To study the refraction of property of light from one medium to another we use the property of intersecting line and parallel line.

Some of the basic terms and definition

Point: A point is shown by dot , an exact location in space.

Line: A line is made of points, a line  is denoted by l, m, n.

Collinear  points If two or more points lies on the same line .

Non Collinear points If two or more points  which do not lies on the same line.

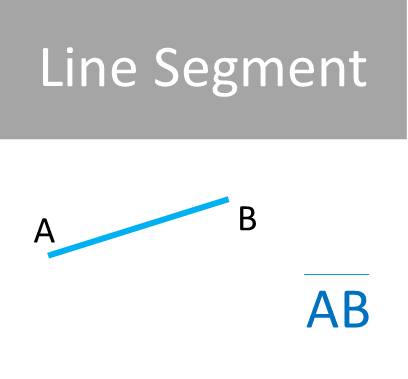
line segment: A line with two end points is called line segment.

 Ray: A part of line with one end is called as ray.

Notation

Point

Angle and there types

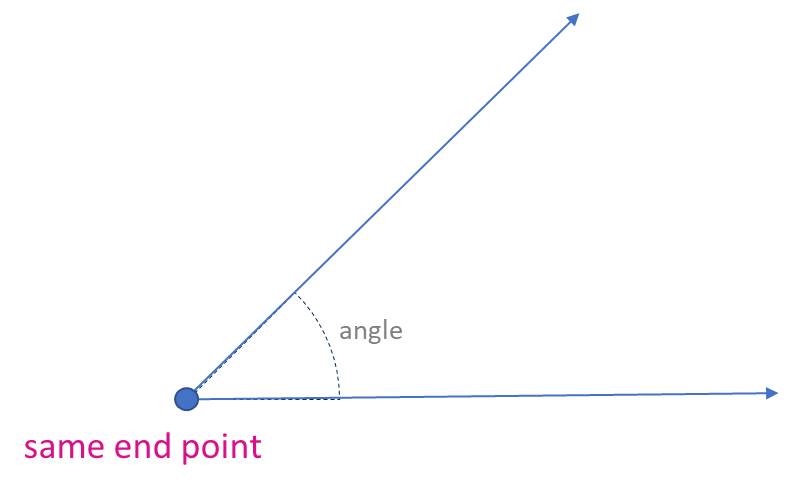
Angle: An angle is formed when two rays  originate from the same end point.

The different types of angles are

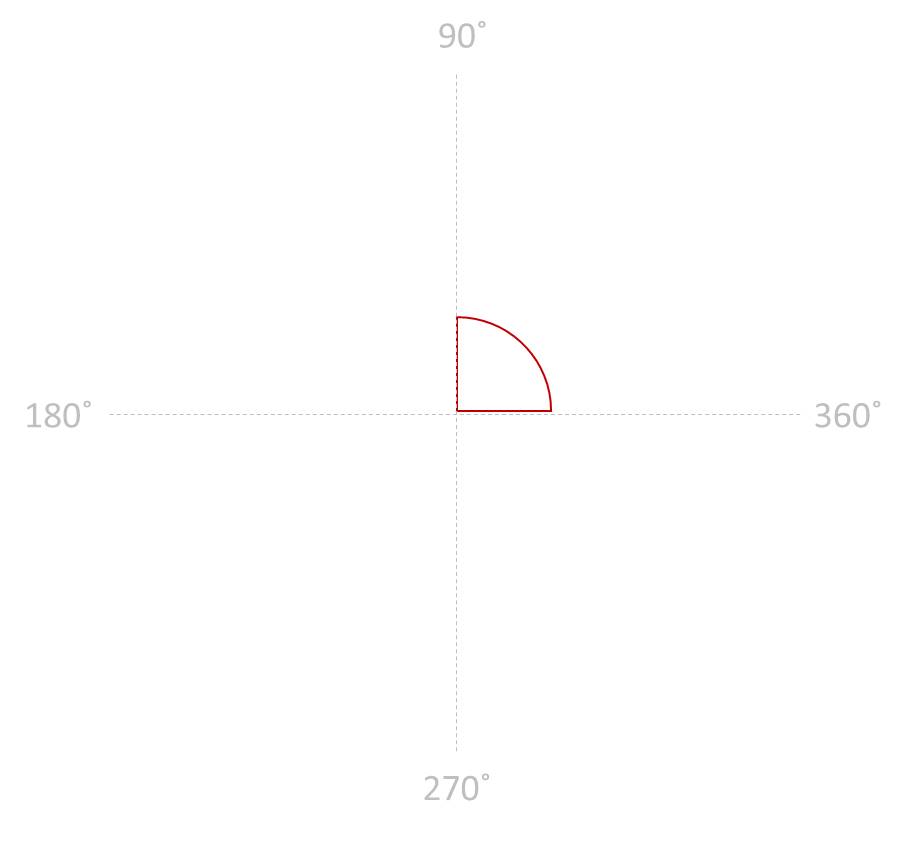
RIGHT ANGLE: An angle that is exactly 90˚

ACUTE ANGLE: An angle that is less than 90˚

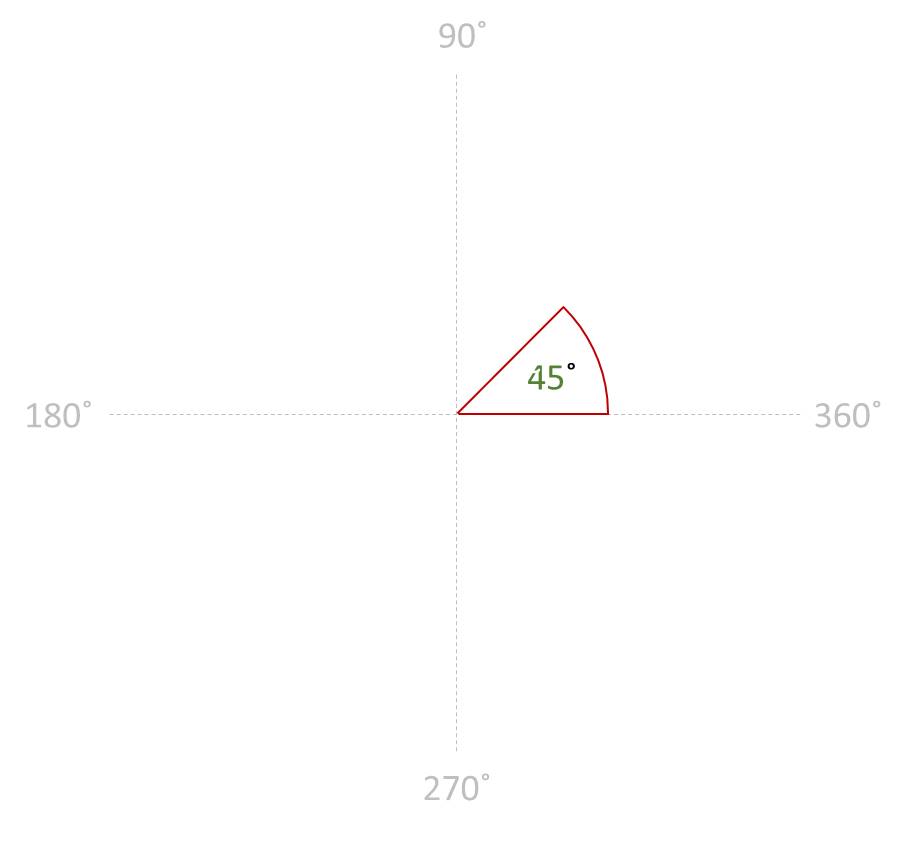
OBTUSE ANGLE: An angle that is greater than90˚and less than 180.

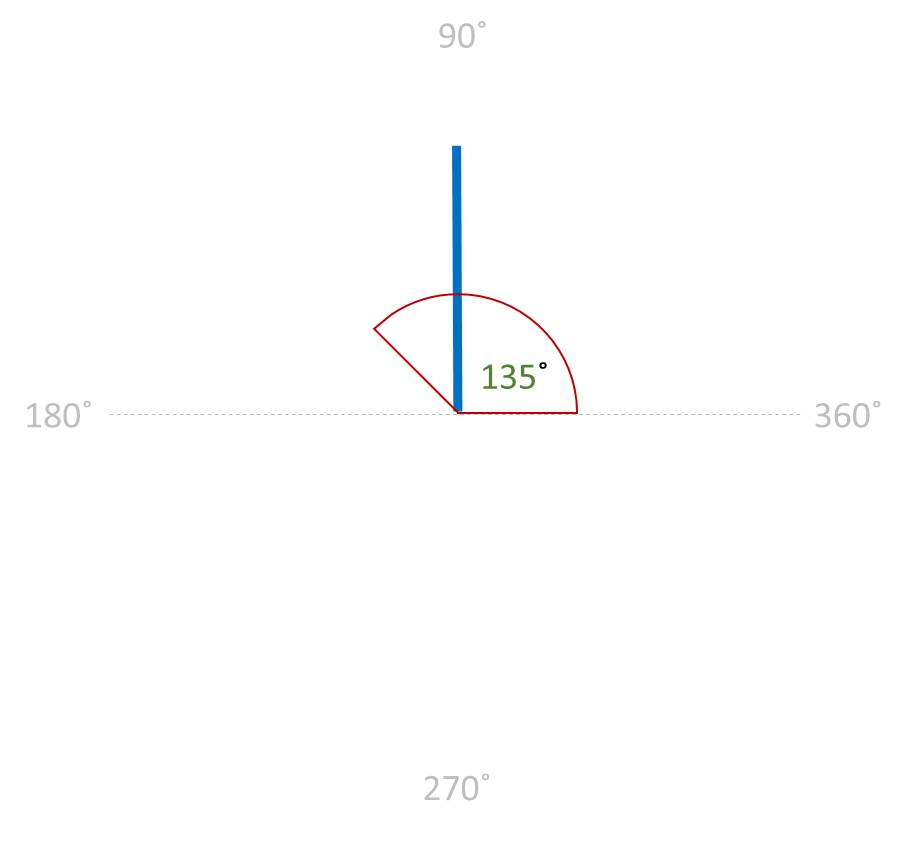
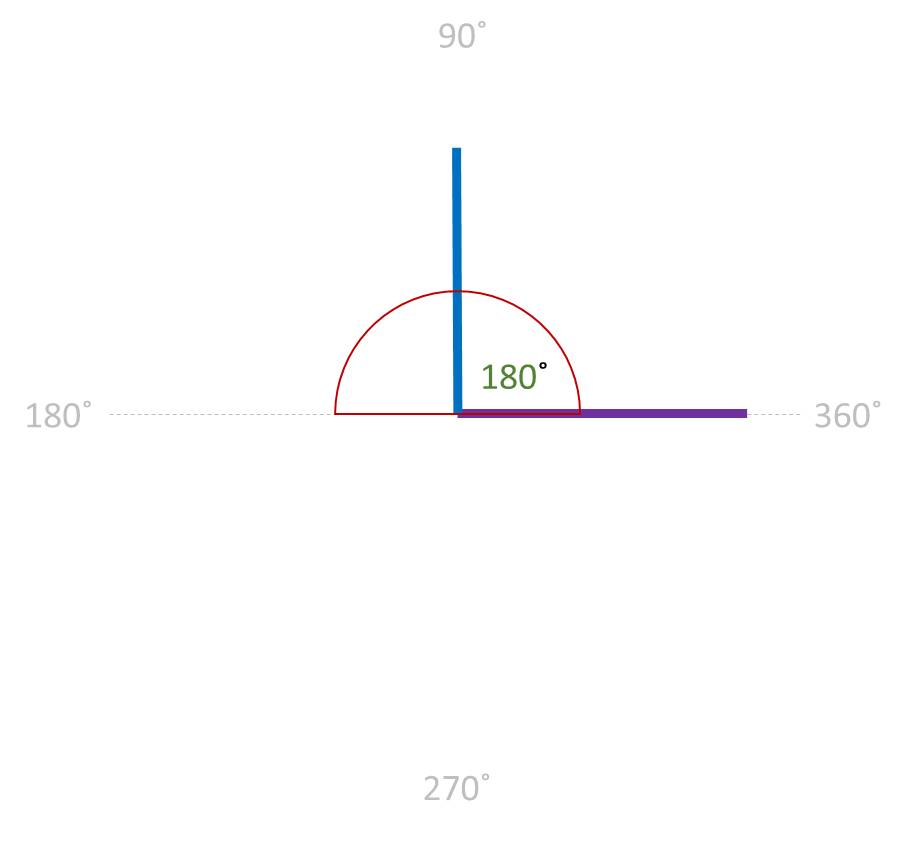
STRAIGHT ANGLE / STRAIGHT LINE: An angle that is exactly 180 ˚

REFLEX ANGLE: An angle that is greater than 180˚
and less than 360 ˚

The sum of two adjacent angels form a pair of 180⁰ is called linear pair of angels.

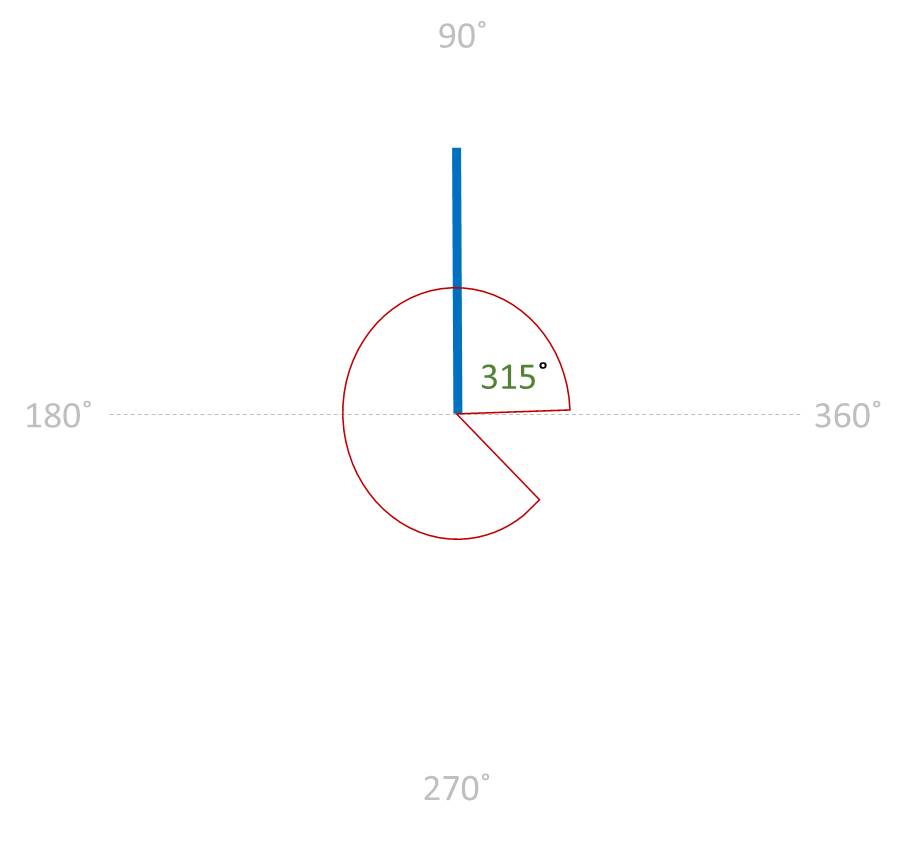
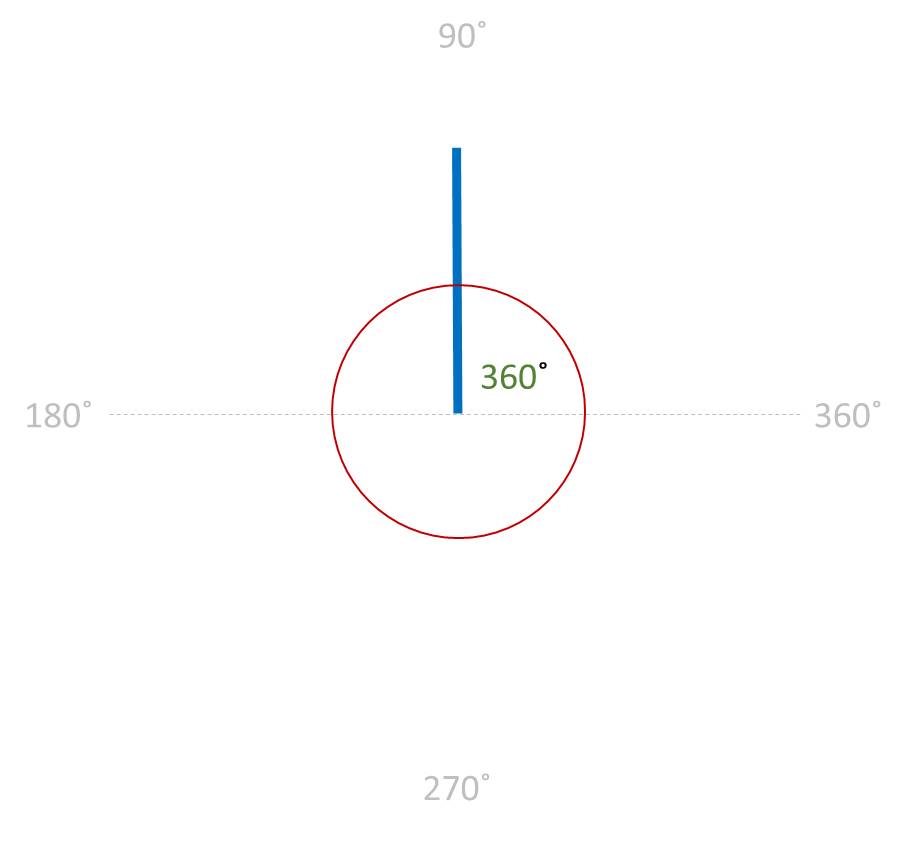
FULL ANGLE: An angle that is exactly 360 ˚

The different types of lines are

1. PARALLEL LINES: They do not intersect when produced indefinitely in either direction

1. INTERSECTING LINES: Are lines that meet a point

PERPENDICULAR LINES: They intersect each other at right angles

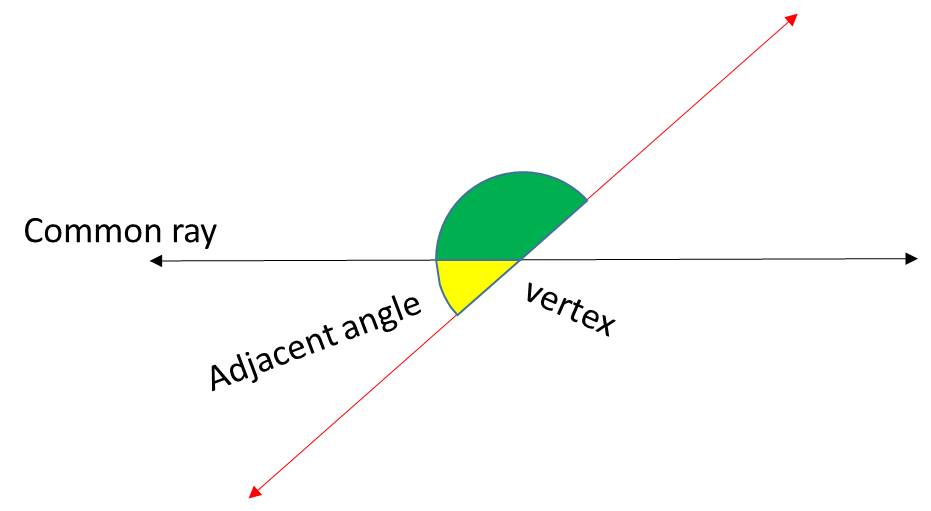
ADJACENT ANGLES:Share a common ray and a common vertex.

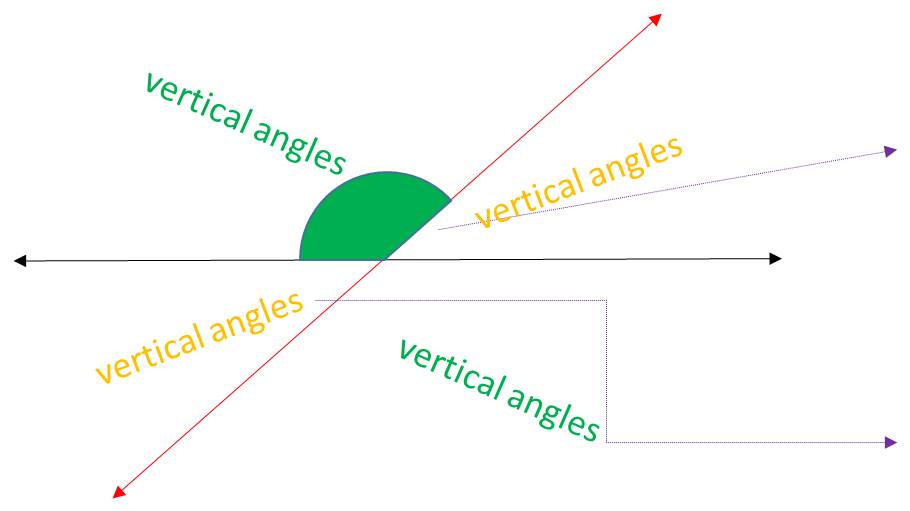
VERTICAL ANGLES: Are pairs of opposite angles made by intersecting lines.

Solved Exercise 3.1

1. In figure, lines AB and CD intersect at 0. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.

Given: ∠AOC + ∠BOE = 70°

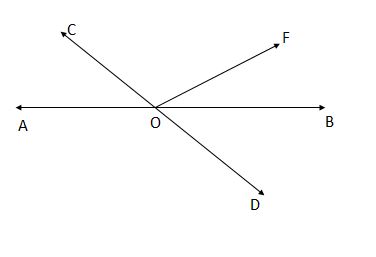
   ∠BOD = 40°

To find: ∠BOE and Reflex ∠COE  

Solution:
Since AB is a straight line,

∴ ∠AOC + ∠COE + ∠EOB = 180°

(∠AOC + ∠BOE) + ∠COE = 180

70° + ∠COE = 180° 

[(Given)]

∠COE = 180° – 70°

           = 110°

∴ Reflex ∠COE = 360° – 110°

             = 250°

AB and CD intersect at O

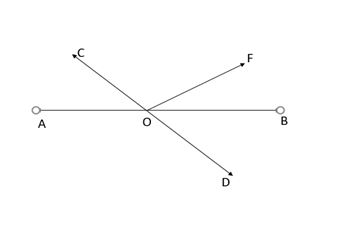
∴∠COA = ∠BOD [Vertically opposite angles

But ∠BOD = 40° [Given]

∴ ∠COA = 40°

Also, ∠AOC + ∠BOE = 70°

∴ 40° + ∠ BOE = 70°

     ∠BOE = 70° -40° = 30°

Thus, ∠BOE = 30° and reflex ∠COE = 250°.

2. In figure, lines XY and MN intersect at 0. If ∠POY = 90° , and a : b = 2 : 3. find c.

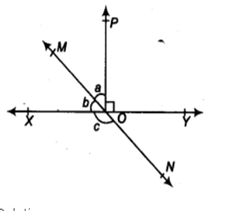
Given:        a : b = 2 : 3 , ∠POY = 90°

To find:      a, b, and c

Solution

Since XOY is a straight line

∴ b+a+∠POY= 180° [ Linear pair]

But ∠POY = 90° [Given]

∴ b + a = 180° – 90°

   b + a = 90°

Let a=2x and b= 3x

Then we have

⇒ 2x + 3x = 90⁰

⇒ 5x= 90⁰

X=90/5

X= 18⁰

Then a= 2x

b= 3x Now c= a + 90⁰ [V O A]

=2 X 18⁰= 36⁰

= 3 x 18⁰ =54⁰

C= 36⁰ + 90⁰ =126⁰

∴ a = 36⁰ , b =  54⁰ and C=126⁰

3. In figure, ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.

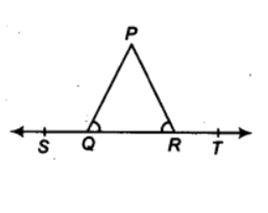
Given:∠PQR = ∠PRQ

To prove:∠PQS = ∠PRT

Proof:ST is a straight line.

∴ ∠PQR + ∠PQS = 180° …(1) [Linear pair]

Similarly, ∠PRT + ∠PRQ = 180° …(2) [Linear Pair]

From (1) and (2), we have

∠PQS + ∠PQR = ∠PRT + ∠PRQ

But ∠PQR = ∠PRQ [Given

∴ ∠PQS = ∠PRT

4. In figure, if x + y = w + ⇒, then prove that AOB is a line

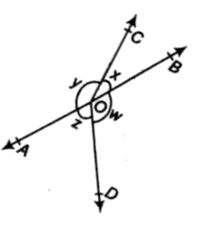
Given: x + y = z + w

To prove:∴ AOB is a straight line

Proof:Sum of all the angles at a point = 360°

x+ y+ z + w = 360⁰ [complete angle]

x + y + x + y = 360⁰ [x + y = z + w]

2x + 2y = 360⁰

2(x + y) = 360⁰

(x + y) =360⁰/2

(x + y) = 180⁰

By linear pair axioms AOB  is a straight line

5. In figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that

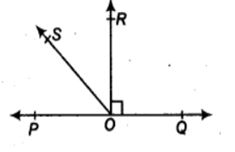
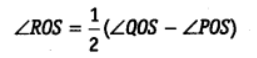
Given

To prove

Proof:

POQ is a straight line. [Given]

POQ is a straight line. [Given]

But OR ⊥ PQ ∴ ∠ROQ = 90°

⇒ ∠POS + ∠ROS + 90° = 180°

⇒ ∠POS + ∠ROS = 90°

⇒ ∠ROS = 90° – ∠POS … (1)

Now, we have ∠ROS + ∠ROQ = ∠QOS

⇒ ∠ROS + 90° = ∠QOS

⇒ ∠ROS = ∠QOS – 90° ……(2)

Adding (1) and (2), we have

2 ∠ROS = (∠QOS – ∠POS)

2 ∠ROS = (∠QOS – ∠POS)

∴ ∠ROS =1/2 (∠QOS – ∠POS)

 6. It is given that ∠XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP, find ∠XYQ and reflex ∠QYP.

Given: ∠XYZ = 64° ,YQ is a bisector of ∠ZYP

To find: ∠XYQ and reflex ∠QYP

Solution:

XYP is a straight line.

∴ ∠XYZ + ∠ZYQ + ∠QYP = 180°

⇒ 64° + ∠ZYQ + ∠QYP = 180° [YQ bisects ∠ZYP so, ∠QYP = ∠ZYQ]

⇒ 2∠QYP = 180° – 64°

⇒ 2∠QYP = 116°

⇒ ∠QYP = “116° ” /2

⇒ ∠QYP = 58°

∴ Reflex ∠QYP = 360° – 58° = 302°

Since ∠XYQ = ∠XYZ + ∠ZYQ

⇒ ∠XYQ = 64° + ∠QYP [∵∠XYZ = 64°(Given) and ∠ZYQ = ∠QYP]

⇒ ∠XYQ = 64° + 58°

   = 122° [∠QYP = 58°]

Thus, ∠XYQ = 122° and reflex ∠QYP = 302°.

Exercise 3.2

1. In figure, find the values of x and y and then show that AB || CD.

To find: values of x and y and AB || CD.

Solution:

In the figure, we have CD and PQ intersect at F

∴ y = 130° …(1)[Vertically opposite angles]

PQ is a straight line and EA stands on it

∠AEP + ∠AEQ = 180° [Linear pair]

50° + x = 180°

⇒ x = 180° – 50°

⇒ x = 130° …(2)

From (1) and (2), x = y = 130°

As they are pair of alternate interior angles.

∴ AB || CD

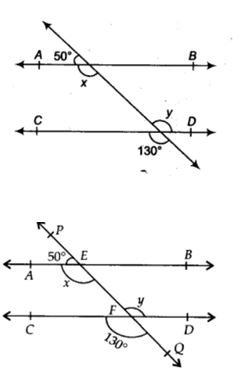
2. In figure, if AB || CD, CD || EF and y : z = 3 : 7, find x.

Given: AB || CD, CD || EF and y : z = 3 : 7

To find: x

Solution:AB || CD, and CD || EF [Given]

∴ AB || EF

∴ x = z [Alternate interior angles] ….(1)⇒ K= “180⁰ ” /10

Again, AB || CD ⇒ K= 18⁰

⇒ x + y = 180° [Co-interior angles Then, Y = 3k, Z = 7k,

⇒ z + y = 180° … (2) [By (1)]

⇒ Y =3 x 18⁰

⇒ Y =54⁰

Z = 7k,

⇒ z = 7 x 18⁰

⇒ Z = 126°

But y : z = 3 : 7

Let k be any variable

3k + 7k =180

10k=180

3. In figure, if AB || CD, EF ⊥ CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.

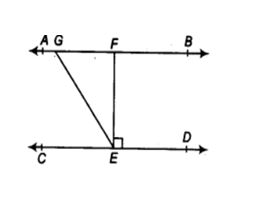
Given: AB || CD, EF ⊥ CD and ∠GED = 126°

To find: ∠AGE, ∠GEF and ∠FGE.

Solution:AB || CD and GE is a transversal.

∴ ∠AGE = ∠GED [Alternate interior angles

But ∠GED = 126° [Given

∴∠AGE = 126°

Also, ∠GEF + ∠FED = ∠GED

∠GEF + 90° = 126° [∵ EF ⊥ CD (given)]

x = z [Alternate interior angles]… (1) Again, AB || CD

⇒ x + y = 180° [Co-interior angles]

∠GEF = 126° -90° = 36°

Now, AB || CD and GE is a transversal

∴ ∠FGE + ∠GED = 180° [Co-interior angles

∠FGE + 126° = 180°

∠FGE = 180° – 126° = 54°

Thus, ∠AGE = 126°,

           ∠GEF= 36° and ∠FGE = 54°.

4. In figure, if PQ || ST, ∠ PQR = 110° and ∠ RST = 130°, find ∠QRS.

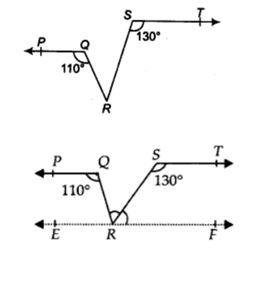
Given: PQ || ST, ∠ PQR = 110° and ∠ RST = 130°

To find: ∠QRS.

Solution:Draw a line EF parallel to ST through R.

Since PQ || ST [Given]
    and EF || ST [Construction]
∴ PQ || EF and QR is a transversal

⇒ ∠PQR = ∠QRF [Alternate interior angles]

 But ∠PQR = 110° [Given]
∴∠QRF = ∠QRS + ∠SRF = 110° …(1)
Again ST || EF and RS is a transversal

∴ ∠RST + ∠SRF = 180° [Co-interior angles]  

      130° + ∠SRF = 180°⇒ ∠SRF = 180° – 130° = 50°

⇒ ∠QRS = 110° – 50° = 60°=Thus, ∠QRS = 60°.
Now, from (1), we have ∠QRS + 50° = 110°

5. In figure, if AB || CD, ∠APQ = 50° and ∠PRD = 127°, find x and y

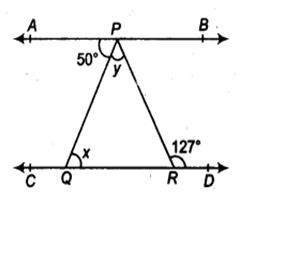
Given: AB || CD, ∠APQ = 50° and ∠PRD = 127°,

To find: x and y.

Solution: We have AB || CD and PQ is a transversal

∴ ∠APQ = ∠PQR            [Alternate interior angles]

⇒ 50° = x [ ∵ ∠APQ = 50° (given)]

AB || CD and PR is a transversal.
∴ ∠APR = ∠PRD [Alternate interior angles]

⇒ ∠APR = 127° [ ∵ ∠PRD = 127° (given)]

⇒ ∠APQ + ∠QPR = 127°
⇒ 50° + y = 127° [ ∵ ∠APQ = 50° (given)]
⇒ y = 127°- 50° = 77°
Thus, x = 50° and y = 77°.

6. In figure, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.

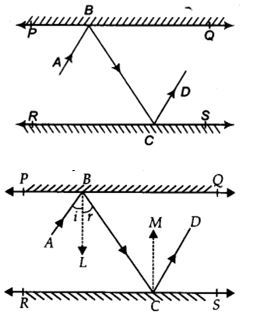
Given:

To find:

CONSTRUCTION: Draw ray BL ⊥PQ and CM ⊥ RS

Solution:∵ PQ || RS ⇒ BL || CM  [∵ BL || PQ and CM || RS]
Now, BL || CM and BC is a transversal.

∴ ∠LBC = ∠MCB …(1) [Alternate interior angles]
Since, angle of incidence = Angle of reflection
∠ABL = ∠LBC and ∠MCB = ∠MCD
⇒ ∠ABL = ∠MCD …(2) [By (1)]
Adding (1) and (2), we get
∠LBC + ∠ABL = ∠MCB + ∠MCD
⇒ ∠ABC = ∠BCD

i.e., a pair of alternate interior angles are equal.
∴ AB || CD.

Angle Sum Property of Triangle:

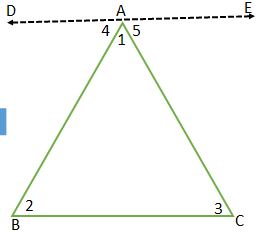
STATEMENT: The sum of the angles of a triangle is 180º.

Given: A  Δ ABC.

To Prove:  ∠1 + ∠2 + ∠3 = 180°

Construction:  Let us draw a line DAE  parallel to BC.

Proof: Statement Reason

DAE ||BC and PQ and AB Is the transversal

Hence, ∠4 = ∠2 (alternate interior angles)

  DAE ||BC and AC Is the transversal (alternate interior angles

  ∠5 = ∠3

Now, DAE is a straight line

∠4 + ∠1 +∠5 = 180°

⇒ ∠1 + ∠4 +∠5 = 180°

Angles on the same side

of DAE at the point A

∠4 = ∠2  and  ∠5 = ∠3

Hence, the sum of the angles of a triangles 180°

Exterior angle property of a triangle theorem

STATEMENT: If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.

Given: A  Δ  ABC. whose side BC has been produced to D.

  Forming exterior angle ∠ACD

To Prove:  ∠ACD = ∠BAC + ∠CBA  [∠4 = ∠1 + ∠2

Proof:. Statement Reason

We know that Δ  ABC from the angle sum property

 ∠1 + ∠2 + ∠3 = 180°…..(i)

Also   ∠3 +∠4 = 180°…..(ii) form a linear pair

From equation (i) and (ii) it follows that:

∠3 +∠4 = ∠1 + ∠2 + ∠3

∴ ∠4 = ∠1 + ∠2

Hence, proved

1. In figure, sides QP and RQ of ∆PQR are produced to points S and T,   respectively. If ∠SPR = 135° and ∠PQT = 110°, find ∠PRQ.

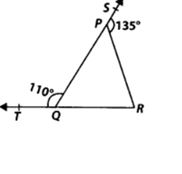
Given:  ∠SPR = 135° and ∠PQT = 110°,

To find: ∠PRQ.

Solution:We have, ∠TQP + ∠PQR = 180°  [Linear pair]

⇒ 110° + ∠PQR = 180°
⇒ ∠PQR = 180° – 110° = 70°

Since, the side QP of ∆PQR is produced to S.

⇒ ∠PQR + ∠PRQ = 135°
[Exterior angle property of a triangle]

⇒ 70° + ∠PRQ = 135° [∠PQR = 70°]
⇒ ∠PRQ = 135° – 70° ⇒ ∠PRQ = 65°

2. In figure, ∠X = 62°, ∠XYZ = 54°, if YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ∆XYZ, find ∠OZY and ∠YOZ.

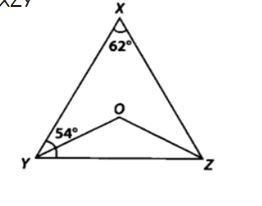
Given: ∠X = 62°, ∠XYZ = 54°, YO and ZO are the bisectors of ∠XYZ and ∠XZY

To find:∠OZY and ∠YOZ.

Solution:In ∆XYZ, we have ∠XYZ + ∠YZX + ∠ZXY = 180°
[Angle sum property of a triangle]

But ∠XYZ = 54° and ∠ZXY = 62°

∴ 54° + ∠YZX + 62° = 180°

⇒ ∠YZX = 180° – 54° – 62° = 64°

YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively.

∴ ∠OYZ = ∠XYZ/ 2 = 54°/ 2 = 27°
and ∠OZY = ∠YZX / 2 = 64°/ 2 = 32°

in ∆OYZ, we have
∠YOZ + ∠OYZ + ∠OZY = 180° [Angle sum property of a triangle

⇒ ∠YOZ + 27° + 32° = 180°
⇒ ∠YOZ = 180° -27° – 32° = 121°

Thus, ∠OZY = 32° and ∠YOZ = 121°

3. In figure, if AB || DE, ∠BAC = 35° and ∠CDE = 53°  , find ∠DCE.

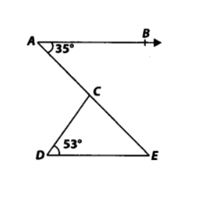
Given: AB || DE, ∠BAC = 35° and ∠CDE = 53°

To find: ∠DCE.

Solution:AB || DE and AE is a transversal.
So, ∠BAC = ∠AED  [Alternate interior angles]

and ∠BAC = 35° [Given]
     ∴ ∠AED = 35°

 in ∆CDE, we have

 ∠CDE + ∠DEC + ∠DCE = 180°     [Angle sum property of a triangle]

∴ 53° + 35° + ∠DCE =180°[∵ ∠DEC = ∠AED = 35° and∠CDE = 53° (Given)]

⇒ ∠DCE = 180° – 53° – 35° = 92°
Thus, ∠DCE = 92°

4. In figure, if lines PQ and RS intersect at point T, such that ∠ PRT = 40°, ∠ RPT = 95° and

∠TSQ = 75°, find ∠ SQT.

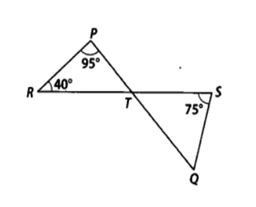
Given: ∠PRT = 40°, ∠ RPT = 95° and ∠TSQ = 75°  

To find: ∠SQT.

Solution:

In ∆PRT, we have ∠P + ∠R + ∠PTR = 180°[Angle sum property of a triangle]

⇒ 95° + 40° + ∠PTR =180° [ ∵ ∠P = 95°, ∠R = 40° (given)]

⇒ ∠PTR = 180° – 95° – 40° = 45°
But PQ and RS intersect at T.

∴ ∠PTR = ∠QTS [Vertically opposite angles

∴ ∠QTS = 45° [ ∵ ∠PTR = 45°]

in ∆ TQS, we have ∠TSQ + ∠STQ + ∠SQT = 180° [Angle sum property of a triangle]

∴ 75° + 45° + ∠SQT = 180° [ ∵ ∠TSQ = 75° and ∠STQ = 45°]

⇒ ∠SQT = 180° – 75° – 45° = 60°
Thus, ∠SQT = 60°

5. In figure, if PQ ⊥ PS, PQ||SR, ∠SQR = 2S° and ∠QRT = 65°, then find the values of x and y.

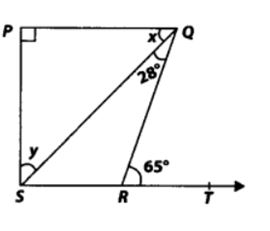
Given

To find:

Solution: In ∆ QRS, the side SR is produced to T.

∴ ∠QRT = ∠RQS + ∠RSQ [Exterior angle property of a triangle]

But ∠RQS = 28° and ∠QRT = 65°

So, 28° + ∠RSQ = 65°
⇒ ∠RSQ = 65° – 28° = 37°

Since, PQ || SR and QS is a transversal.

∴ ∠PQS = ∠RSQ = 37° [Alternate interior angles]

⇒ x = 37°

PQ ⊥ PS ⇒ AP = 90°
 in ∆PQS, ∠P + ∠PQS + ∠PSQ = 180° [Angle sum property of a triangle]

⇒ 90° + 37° + y = 180°

⇒ y = 180° – 90° – 37° = 53°

Thus, x = 37° and y = 53°

6. In figure, the side QR of ∆PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR

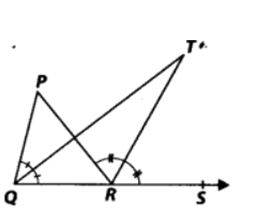
Solution:In ∆PQR, side QR is produced to S, so by exterior angle property, ∠PRS = ∠P + ∠PQR

⇒ 1/2∠PRS = 1/2∠P + 12∠PQR

Now⇒ ∠TRS = 1/2∠P + ∠TQR …(1)[∵ QT and RT are bisectors of ∠PQR and   ∠PRS respectively.]

∠TRS = ∠TQR + ∠T …(2)[Exterior angle property of a triangle]

From (1) and (2),

we have ∠TQR + 1/2∠P = ∠TQR + ∠T

⇒ 1/2∠P = ∠T

⇒ 1/2∠QPR = ∠QTR or ∠QTR = 1/2∠QPR