ರೇಖೆಗಳು ಮತ್ತು ಕೋನಗಳು

ಬಿಂದುಗಳು

ಬಿಂದುವನ್ನು ಚುಕ್ಕಿಯಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ.

ಒಂದು ಬಿಂದುವು ಒಂದು ಸ್ಥಳವನ್ನು ನಿರ್ಧರಿಸುತ್ತದೆ.

ಸಾಮಾನ್ಯ ಬಿಂದುವನ್ನು ಶೃಂಗಬಿಂದು ಎನ್ನುತ್ತೇವೆ

---

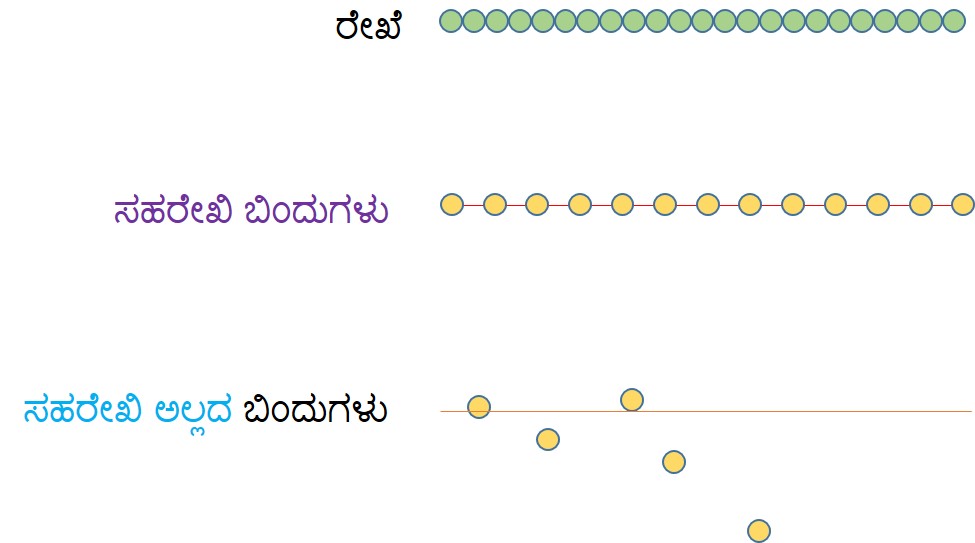
ಒಂದು ರೇಖೆಯು ಹಲವಾರು ಬಿಂದುಗಳಿಂದಾಗಿರುತ್ತದೆ.

ಸಹರೇಖಿ ಬಿಂದುಗಳು ಒಂದು ಸರಳ ರೇಖೆಯ ಮೇಲೆ ಸಮಾನವಾಗಿ ಹರಡಿಕೊಂಡಿರುತ್ತವೆ.

ಸಹರೇಖಿ ಅಲ್ಲದ ಬಿಂದುಗಳು ಒಂದೇ ಸರಳರೇಖೆಯ ಮೇಲೆ ಇರುವುದಿಲ್ಲ.

---

ರೇಖಾಖಂಡ

ಎರಡು ಅಂತ್ಯಬಿಂದುಗಳನ್ನು ಹೊಂದಿರುವ ಸರಳರೇಖೆಯ ಒಂದು ಭಾಗವನ್ನು ರೇಖಾಖಂಡ ಎನ್ನುತ್ತಾರೆ

ರೇಖೆ

ರೇಖೆಯನ್ನು ಎರಡು ತುದಿಗಳಲ್ಲಿ  ವಿಸ್ತರಿಸಬಹುದು

ರೇಖಾಕಿರಣ

ರೇಖಾಕಿರಣವು ಆರಂಭ ಬಿಂದುವನ್ನು ಹೊಂದಿರುತ್ತದೆ, ಅಂತ್ಯ ಬಿಂದು ಇರುವುದಿಲ್ಲ   ಮತ್ತು ಒಂದು ದಿಕ್ಕಿನಲ್ಲಿ ಅಂತ್ಯವಿಲ್ಲದಂತೆ ಮುಂದುವರೆಯುತ್ತದೆ

---

---

ಸಂಕೇತನ ಕೋನಗಳು

ಒಂದೇ  ಬಿಂದುವಿನಿಂದ ಹೊರಟ ಎರಡು ರೇಖಾಕಿರಣಳಿಂದ ಕೋನವುಂಟಾಗುವುದು

ಲಂಬಕೋನ

 ಕೋನವು ಸರಿಯಾಗಿ 90˚ಗೆ ಸಮವಾಗಿರುತ್ತದೆ

ಲಘು ಕೋನ

ಕೋನವು 0˚ ಮತ್ತು  90˚ಗೆ ನಡುವೆ ಇರುತ್ತದೆ

ಅಧಿಕ  ಕೋನ

ಕೋನವು 90˚ಗಿಂತ ಹೆಚ್ಚು  ಮತ್ತು  180˚ಗಿಂತ  ಕಡಿಮೆ  ಇರುತ್ತದೆ

ಸರಳ ಕೋನ

ಕೋನವು ಸರಿಯಾಗಿ 180˚ಗೆ ಸಮವಾಗಿರುತ್ತದೆ

ಸರಳಾಧಿಕ   ಕೋನ

ಕೋನವು 180˚ಗಿಂತ ಹೆಚ್ಚು ಮತ್ತು  360˚ಗಿಂತ  ಕಡಿಮೆ  ಇರುತ್ತದೆ

ಪೂರ್ಣ  ಕೋನ

ಕೋನವು ಸರಿಯಾಗಿ  360˚ಗೆ ಸಮವಾಗಿರುತ್ತದೆ

ಸಮಾಂತರ  ರೇಖೆಗಳು

ಎರಡು ಸರಳರೇಖೆಗಳನ್ನೂ ಅನಂತ ದೂರದವರೆಗೆ ವೃದ್ದಿಸಿದಾಗಲೂ ಪರಸ್ಪರ ಛೇದಿಸುವುದಿಲ್ಲ

ಛೇದಿಸುವ ರೇಖೆಗಳು

ಸಮಾನ ಬಿಂದುವಿನಲ್ಲಿ ಎರಡು ಸರಳ ರೇಖೆಗಳು ಪರಸ್ಪರ ಛೇದಿಸುವ ರೇಖೆಗಳು

ಲಂಬರೇಖೆಗಳು

ರೇಖೆಗಳು ಪರಸ್ಪರ ಲಂಬಕೋನದಲ್ಲಿ (90˚) ಛೇದಿಸುತ್ತವೆ

---

---

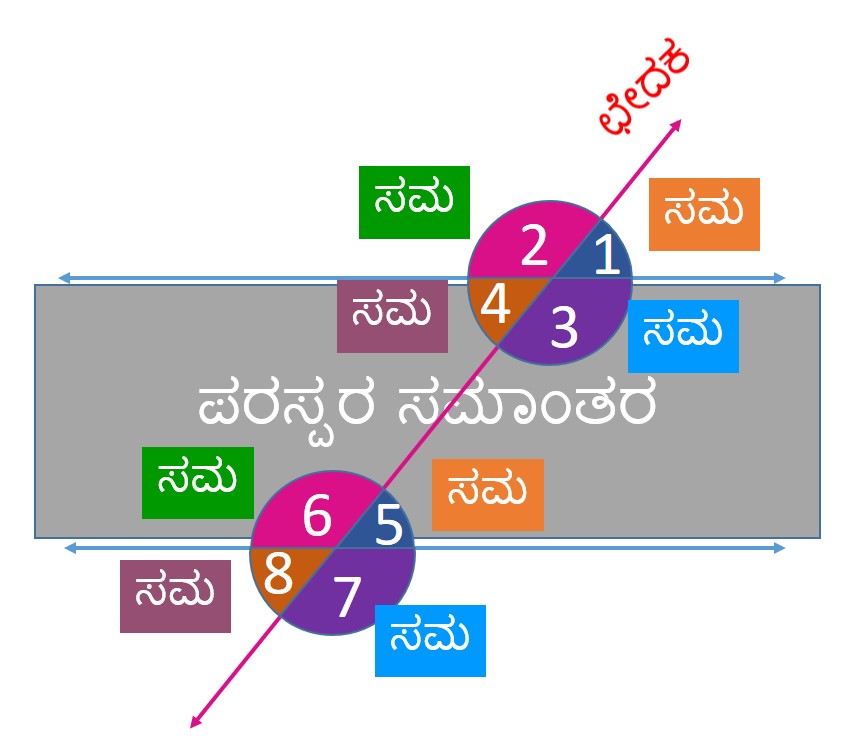
ಪಾರ್ಶ್ವ ಕೋನಗಳು

ಯಾವುದೇ ಎರಡು ಕೋನಗಳು ಉಭಯ ಸಾಮಾನ್ಯ ಬಾಹು, ಒಂದು ಉಭಯ ಸಾಮಾನ್ಯ ಶೃಂಗ ಬಿಂದುವನ್ನು ಹೊಂದಿದ್ದರೆ, ಅಂತಹ ಕೋನಗಳನ್ನು ‘ಪಾರ್ಶ್ವ ಕೋನಗಳು’ ಎನ್ನುತ್ತೇವೆ

ಶೃಂಗಾಭಿಮುಖ ಕೋನಗಳು

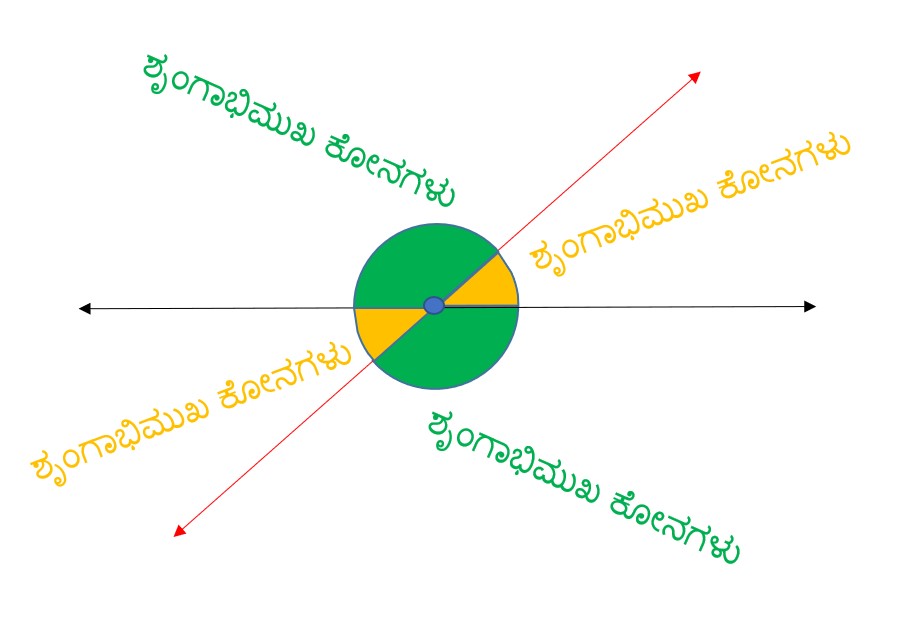
ಎರಡು ಸರಳರೇಖೆಗಳು ಪರಸ್ಪರ ಛೇದಿಸಿದಾಗ ಉಂಟಾಗುವ ಕೋನಗಳು

ಛೇದಿಸುವ ರೇಖೆಗಳಿಂದ ವಿರುದ್ಧ ದಿಕ್ಕಿನಲ್ಲಿ ಉಂಟಾಗುವ ಕೋನಗಳು

ಶೃಂಗಾಭಿಮುಖ ಕೋನಗಳು ಸಮನಾಗಿರುತ್ತವೆ

ಪೂರಕ ಕೋನಗಳು

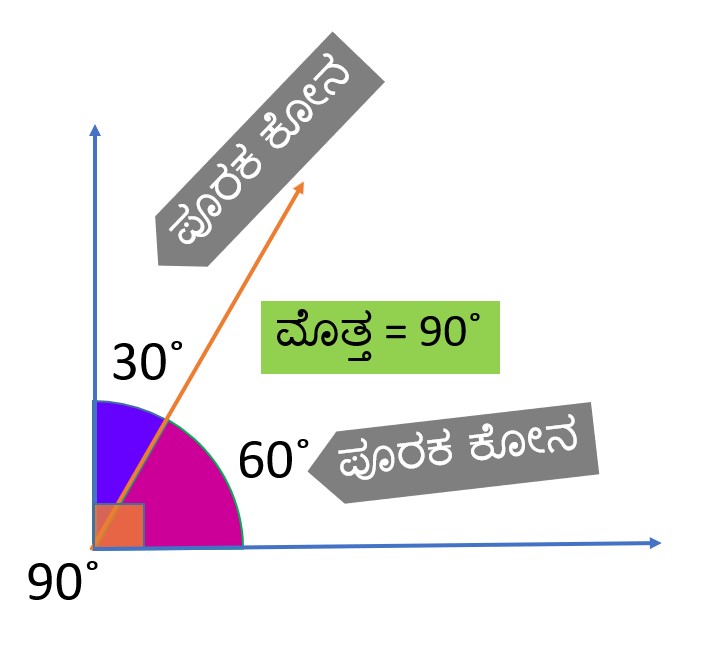
ಎರಡು ಕೋನಗಳ ಮೊತ್ತ 90˚ ಇದ್ದರೆ, ಆ ಎರಡು ಕೋನಗಳನ್ನು ಪೂರಕ ಕೋನಗಳು (complimentary) ಎನ್ನುತ್ತೇವೆ

ಇಲ್ಲಿ 60˚ ಮತ್ತು 30˚ ಅಳತೆಯ ಕೋನಗಳು ಪೂರಕ ಕೋನಗಳಾಗಿವೆ

ಎರಡು ಪೂರಕ ಕೋನಗಳನ್ನು ಪರಸ್ಪರ ಪೂರಕ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ

ಪರಿಪೂರಕ ಕೋನಗಳು (ಅಥವಾ ಸಂಪೂರಕ ಕೋನಗಳು)

ಎರಡು ಕೋನಗಳ ಮೊತ್ತ 180˚ ಇದ್ದರೆ, ಆ ಎರಡು ಕೋನಗಳನ್ನು “ಪರಿಪೂರಕ ಕೋನಗಳು” (ಅಥವಾ ಸಂಪೂರಕ ಕೋನಗಳು)(supplementary) ಎನ್ನುತ್ತೇವೆ

ಇಲ್ಲಿ 62˚ ಮತ್ತು 118˚ ಅಳತೆಯ ಕೋನಗಳು ಸಂಪೂರಕ ಕೋನಗಳಾಗಿವೆ

ಎರಡು ಸಂಪೂರಕ ಕೋನಗಳನ್ನು ಪರಸ್ಪರ ಸಂಪೂರಕ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ

ಪಾರ್ಶ್ವ ಕೋನಗಳು

ಒಂದು ಸಾಮಾನ್ಯ ಶೃಂಗ, ಒಂದು ಸಾಮಾನ್ಯ ಬಾಹು ಮತ್ತು ಸಾಮಾನ್ಯವಲ್ಲದ ಎರಡು ಬಾಹುಗಳು ಸಾಮಾನ್ಯ ಬಾಹುವಿನ ವಿವಿಧ ಕಡೆ ಇದ್ದಾಗ ಉಂಟಾಗುವ ಕೋನಗಳನ್ನು   ಪಾರ್ಶ್ವಕೋನಗಳು ಎನ್ನುತ್ತೇವೆ (adjacent angles)

ಅವುಗಳ ಸಾಮಾನ್ಯವಲ್ಲದ ಬಾಹುಗಳು ಸಾಮಾನ್ಯ ಬಾಹುವಿನ ಎರಡೂ ಬದಿಯಲ್ಲಿವೆ

ಸರಳಯುಗ್ಮ ಕೋನಗಳು

ಒಂದು ಸರಳರೇಖೆಯ ಮೇಲೆ ಒಂದು ರೇಖಾಕಿರಣ ನಿಂತಾಗ ಆ ಸಾಮಾನ್ಯ ಬಿಂದುವಿನಲ್ಲಿ ಉಂಟಾಗುವ ಕೋನಗಳ ಮೊತ್ತ 180˚  ಇರುತ್ತದೆ. ಆ ಕೋನಗಳನ್ನು ಸರಳಯುಗ್ಮ ಕೋನಗಳು ಎನ್ನುತ್ತೇವೆ.

ಶೃಂಗಾಭಿಮುಖ ಕೋನಗಳು

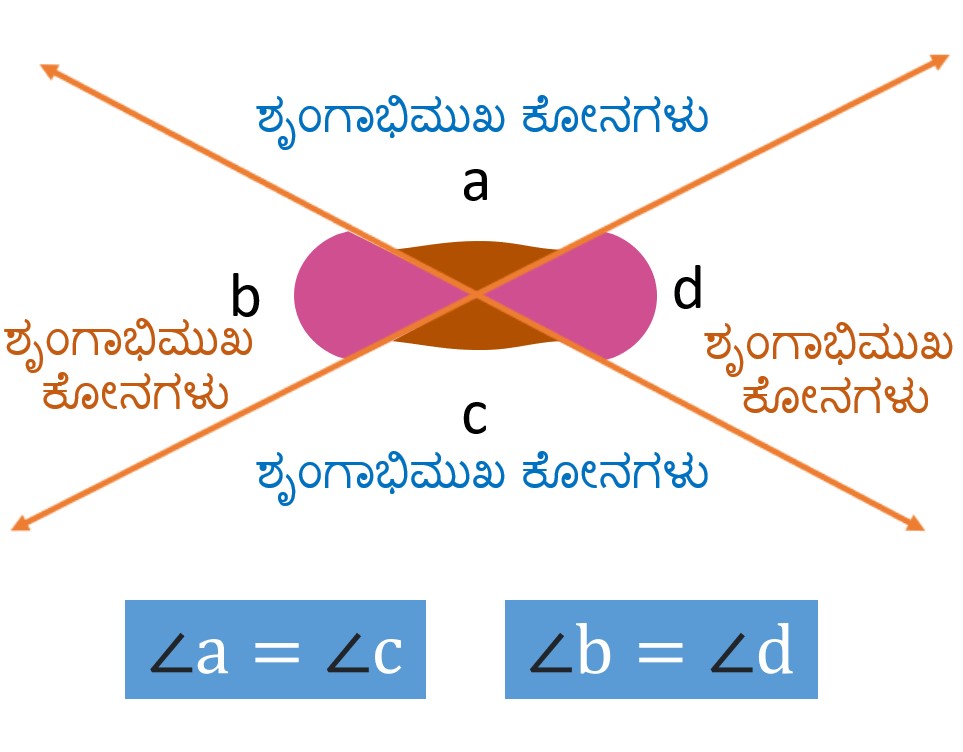
ಎರಡು ಸರಳರೇಖೆಗಳು ಪರಸ್ಪರ ಛೇದಿಸಿದಾಗ ಉಂಟಾಗುವ ಶೃಂಗಾಭಿಮುಖ ಕೋನಗಳು

ಶೃಂಗಾಭಿಮುಖ ಕೋನಗಳು ಪರಸ್ಪರ ಸಮವಾಗಿರುತ್ತವೆ

ಛೇದಕ ರೇಖೆ

ಒಂದೇ ಸಮತಲದಲ್ಲಿರುವ ಎರಡು ಸರಳ ರೇಖೆಗಳನ್ನು ಬೇರೆ ಬೇರೆ ಬಿಂದುಗಳಲ್ಲಿ ಛೇದಿಸುವ ರೇಖೆಯನ್ನು ‘ಛೇದಕ ರೇಖೆ’ (transversal) ಎನ್ನುವರು

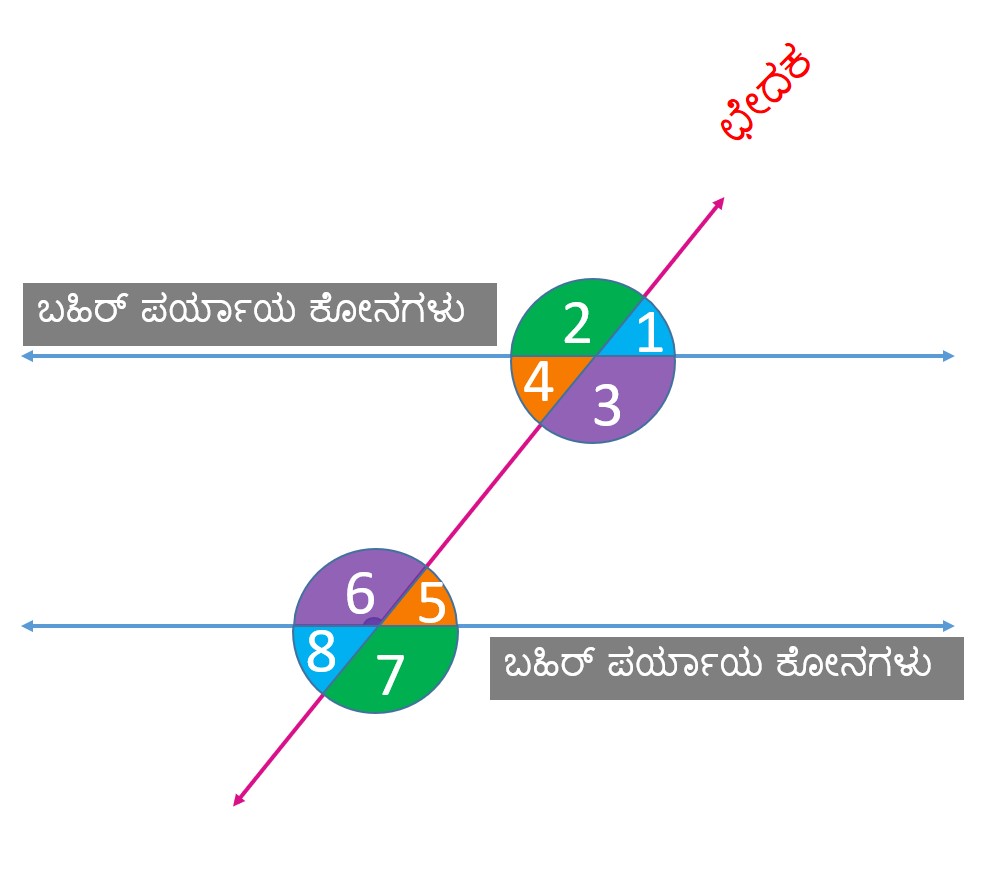
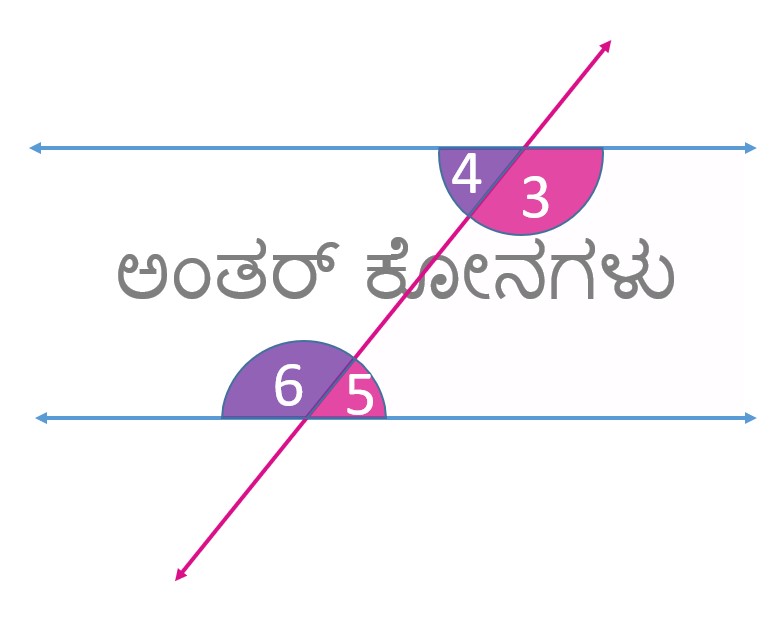
ಅಂತರ್ ಕೋನಗಳು & ಬಹಿರ್ ಕೋನಗಳು

3, 4, 5 and 6 ಅಂತರ್ ಕೋನಗಳು

1, 2, 7 and 8 ಬಹಿರ್ ಕೋನಗಳು

ಒಂದು ಛೇದಕವು ಒಂದು ಜೊತೆ ಅಂತರ್ ಕೋನಗಳು ಹಾಗು ಒಂದು ಜೊತೆ ಬಹಿರ್ ಕೋನಗಳನ್ನು  ಉಂಟು ಮಾಡುತ್ತದೆ.

ಛೇದಕದಿಂದ ಉಂಟಾಗುವ ಕೋನಗಳು

ಒಂದು ಛೇದಕ ರೇಖೆಯು ಎರಡು ಸಮಾಂತರ ಸರಳರೇಖೆಗಳನ್ನು ಛೇದಿಸಿದಾಗ ಉಂಟಾಗುವ ಅನುರೂಪಕೋನಗಳು ಸಮವಾಗಿರುತ್ತದೆ

ಪರ್ಯಾಯ ಅಂತರ್ ಕೋನಗಳು & ಪರ್ಯಾಯ ಬಹಿರ್ ಕೋನಗಳು

ಎರಡು ಸಮಾಂತರ ರೇಖೆಗಳನ್ನು ಒಂದು ಛೇದಕವು ಛೇದಿಸಿದಾಗ ಏರ್ಪಡುವ

-ಪ್ರತಿಯೊಂದು ಜೊತೆ ಪರ್ಯಾಯ ಅಂತರ್ ಕೋನಗಳು ಸಮವಾಗಿರುತ್ತವೆ

-ಪ್ರತಿಯೊಂದು ಜೊತೆ ಪರ್ಯಾಯ ಬಹಿರ್ ಕೋನಗಳು ಸಮವಾಗಿರುತ್ತವೆ

ಎರಡು ಸರಳ ರೇಖೆಗಳನ್ನು ಒಂದು ಛೇದಕ ರೇಖೆಯು ಛೇದಿಸಿದಾಗ ಉಂಟಾಗುವ ವಿವಿಧ ಕೋನಗಳು

• ಪಾರ್ಶ್ವ ಕೋನಗಳು
• ಶೃಂಗಾಭಿಮುಖ ಕೋನಗಳು (4 ಜೊತೆ)
• ಪರ್ಯಾಯ ಕೋನಗಳು (2 ಜೊತೆ)
• ಅನುರೂಪ ಕೋನಗಳು (4 ಜೊತೆ)

ಆಧಾರ ಪ್ರತಿಜ್ಞೆಗಳು

---

ಆಧಾರ ಪ್ರತಿಜ್ಞೆ  1 ಒಂದು ಸರಳರೇಖೆಯ ಮೇಲೆ ಒಂದು ಕಿರಣವು ನಿಂತಾಗ ಉಂಟಾಗುವ ಪಾರ್ಶ್ವಕೋನಗಳ ಮೊತ್ತ 180˚

---

ಆಧಾರ ಪ್ರತಿಜ್ಞೆ 2 ಎರಡು ಪಾರ್ಶ್ವಕೋನಗಳ ಮೊತ್ತವು ೧೮೦ ಆದರೆ, ಆ ಕೋನಗಳ ಸಾಮಾನ್ಯವಲ್ಲದ ಬಾಹುಗಳು ಸರಳರೇಖೆಯನ್ನು ಉಂಟುಮಾಡುತ್ತವೆ

ಎರಡು ಪಾರ್ಶ್ವಕೋನಗಳ ಮೊತ್ತವು 180 ಆದಾಗ ಅವುಗಳನ್ನು  ಸರಳಯುಗ್ಮಗಳು ಎನ್ನಲಾಗುತ್ತದೆ.

ಆದ್ದರಿಂದ ಈ ಮೇಲಿನ ಎರಡು ಆಧಾರ ಪ್ರತಿಜ್ಞೆಗಳನ್ನು ಸರಳಯುಗ್ಮ ಆಧಾರ ಪ್ರತಿಜ್ಞೆಗಳು ಎನ್ನುವರು

---

ಆಧಾರ ಪ್ರತಿಜ್ಞೆ 3 ಒಂದು ಛೇದಕ ರೇಖೆಯು ಎರಡು ಸಮಾಂತರ ಸರಳರೇಖೆಗಳನ್ನು ಛೇದಿಸಿದಾಗ ಉಂಟಾಗುವ ಅನುರೂಪಕೋನಗಳು ಸಮವಾಗಿರುತ್ತದೆ

ಇದನ್ನು ಅನುರೂಪ ಕೋನಗಳು ಆಧಾರ  ಪ್ರತಿಜ್ಞೆ ಎಂದೂ ಸಹ ಕರೆಯುವರು

---

ಆಧಾರ ಪ್ರತಿಜ್ಞೆ 4 ಒಂದು ಛೇದಕವು ಎರಡು ರೇಖೆಗಳನ್ನು ಛೇದಿಸಿದಾಗ ಉಂಟಾಗುವ ಒಂದು ಜೊತೆ ಅನುರೂಪ ಕೋನಗಳು ಸಮವಿದ್ದಾಗ ಆ ಎರಡು ರೇಖೆಗಳು ಪರಸ್ಪರ ಸಮಾಂತರವಾಗಿರುತ್ತವೆ

---

ಪ್ರಮೇಯಗಳು

ಪ್ರಮೇಯ 1 ಎರಡು ಸರಳರೇಖೆಗಳು ಪರಸ್ಪರ ಛೇದಿಸಿದಾಗ ಉಂಟಾಗುವ ಶೃಂಗಾಭಿಮುಖ ಕೋನಗಳು ಪರಸ್ಪರ ಸಮವಾಗಿರುತ್ತವೆ

---

ಪ್ರಮೇಯ 2  ಎರಡು ಸಮಾಂತರ ರೇಖೆಗಳನ್ನು ಒಂದು ಛೇದಕವು ಛೇದಿಸಿದಾಗ ಏರ್ಪಡುವ ಪ್ರತಿಯೊಂದು ಜೊತೆ ಪರ್ಯಾಯ ಅಂತರ್ ಕೋನಗಳು ಸಮವಾಗಿರುತ್ತವೆ

---

ಪ್ರಮೇಯ 3 ಒಂದು ಛೇದಕವು ಎರಡು ರೇಖೆಗಳನ್ನು ಛೇದಿಸಿದಾಗ ಉಂಟಾಗುವ ಒಂದು ಜೊತೆ ಪರ್ಯಾಯ ಅಂತರ್ ಕೋನಗಳು ಸಮವಿದ್ದಾಗ ಆ ಎರಡು ರೇಖೆಗಳು ಪರಸ್ಪರ ಸಮಾಂತರವಾಗಿರುತ್ತವೆ

---

ಪ್ರಮೇಯ 4 ಒಂದು ಛೇದಕವು ಎರಡು ಸಮಾಂತರ ರೇಖೆಗಳನ್ನು ಛೇದಿಸಿದಾಗ, ಛೇದಕದ ಒಂದೇ ಪಾರ್ಶ್ವದಲ್ಲಿರುವ ಪ್ರತಿಯೊಂದು ಜೊತೆ ಅಂತರ್ ಕೋನಗಳು ಸರಳಕೋನ ಪೂರಕಗಳಾಗಿರುತ್ತವೆ

---

ಪ್ರಮೇಯ 5 ಒಂದು ಛೇದಕವು ಎರಡು ರೇಖೆಗಳನ್ನು ಛೇದಿಸಿದಾಗ, ಛೇದಕದ ಒಂದೇ ಪಾರ್ಶ್ವದಲ್ಲಿರುವ ಪ್ರತಿಯೊಂದು ಜೊತೆ ಅಂತರ್ ಕೋನಗಳು ಸರಳಕೋನ ಪೂರಕಗಳಾಗಿದ್ದರೆ, ಆ ಎರಡು ರೇಖೆಗಳು ಸಾಮಂತರವಾಗಿರುತ್ತವೆ

---

ಪ್ರಮೇಯ 6  : ಒಂದೇ ರೇಖೆಗೆ ಸಮಾಂತರವಾಗಿರುವ ಎರಡು ರೇಖೆಗಳು ಪರಸ್ಪರ ಸಮಾಂತರವಾಗಿರುತ್ತವೆ

ಪಠ್ಯದ ಅಭ್ಯಾಸಗಳು

ಪಠ್ಯದ ಅಭ್ಯಾಸಗಳು

1.ಚಿತ್ರದಲ್ಲಿ AB ಮತ್ತು CD ಸರಳರೇಖೆಗಳು O ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸುತ್ತಿವೆ. ∠AOC + ∠BOE = 70° ಮತ್ತು ∠BOD = 40° ಆದರೆ ∠BOE ಮತ್ತು ಸರಳಾಧಿಕ ∠COE ಕಂಡುಹಿಡಿಯಿರಿ.

ಕೊಟ್ಟಿರುವಂತೆ : ∠AOC + ∠BOE = 70°

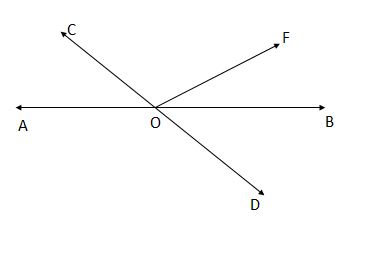
   ∠BOD = 40°

ಕಂಡುಹಿಡಿಯಲು : ∠BOE ಮತ್ತು ಸರಳಾಧಿಕ ∠COE  

ಪರಿಹಾರ :
AB ಒಂದು ಸರಳರೇಖೆಯಾಗಿದೆ. ಆದ್ದರಿಂದ ,

∴ ∠AOC + ∠COE + ∠EOB = 180°

(∠AOC + ∠BOE) + ∠COE = 180

70° + ∠COE = 180° 

(ಕೊಟ್ಟಿರುವಂತೆ)

∠COE = 180° – 70°

           = 110°

∴ ಸರಳಾಧಿಕ∠COE = 360° – 110°

             = 250°

AB ಮತ್ತು CD ‘O’ ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸುತ್ತಿವೆ

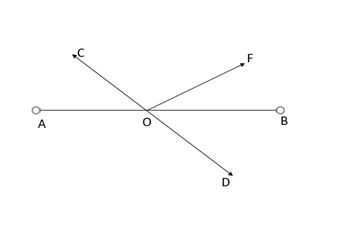
∴∠COA = ∠BOD ಅವು ಶೃಂಗಾಭಿಮುಖ ಕೋನಗಳು ಆಗಿವೆ.

ಆದರೆ ∠BOD = 40° [ಕೊಟ್ಟಿರುವಂತೆ]

∴ ∠COA = 40°

ಹಾಗೂ, ∠AOC + ∠BOE = 70°

∴ 40° + ∠ BOE = 70°

     ∠BOE = 70° -40° = 30°

ಹೀಗೆ , ∠BOE = 30° ಮತ್ತು ಸರಳಾಧಿಕ ∠COE = 250°.

---

2. ಕೆಳಗಿನ ಚಿತ್ರದಲ್ಲಿ XY ಮತ್ತು MN ಸರಳರೇಖೆಗಳು O ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸುತ್ತಿವೆ. ∠POY = 90° ಮತ್ತು : b = 2 : 3 ಆದರೆ c ಕಂಡುಹಿಡಿಯಿರಿ.

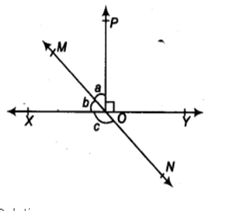
ಕೊಟ್ಟಿರುವಂತೆ:        a : b = 2 : 3 , ∠POY = 90°

ಕಂಡುಹಿಡಿಯಲು:      a, b, ಮತ್ತು c

ಪರಿಹಾರ

XOY ಒಂದು ಸರಳರೇಖೆಯಾಗಿದೆ

∴ b+a+∠POY= 180° [ಸರಳಯುಗ್ಮ ಕೋನಗಳು]

ಆದರೆ ∠POY = 90° [ಕೊಟ್ಟಿರುವಂತೆ]

∴ b + a = 180° – 90°

   b + a = 90°

a : b = 2 : 3 => a=2x ಮತ್ತು b= 3x ಎಂದು ನಾವು ಬರೆಯಬಹುದು.

ಅಂತೆಯೇ

⇒ 2x + 3x = 90⁰ ಆಗುತ್ತದೆ.

⇒ 5x= 90⁰

X=90/5

X= 18⁰

ಅದೇ ರೀತಿ a= 2x

b= 3x ಈಗ c= a + 90⁰ [V O A]

=2 X 18⁰= 36⁰

= 3 x 18⁰ =54⁰

C= 36⁰ + 90⁰ =126⁰

∴ a = 36⁰ , b =  54⁰ and C=126⁰

---

3. ಕೆಳಗಿನ ಚಿತ್ರದಲ್ಲಿ, ∠PQR = ∠PRQ ಆದರೆ ∠PQS = ∠PRT ಎಂದು ಸಾಧಿಸಿ..

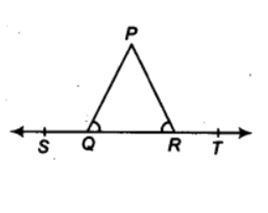
ಕೊಟ್ಟಿರುವಂತೆ: ∠PQR = ∠PRQ

ಸಾಧಿಸಬೇಕಾಗಿರುವುದು: ∠PQS = ∠PRT

ಪುರಾವೆ: ST ಒಂದು ಸರಳರೇಖೆಯಾಗಿದೆ.

∴ ∠PQR + ∠PQS = 180° …(1) [ಸರಳಯುಗ್ಮ ಕೋನಗಳು]

ಅದೇ ರೀತಿಯಾಗಿ , ∠PRT + ∠PRQ = 180° …(2) [ಸರಳಯುಗ್ಮ ಕೋನಗಳು]

(1) ಮತ್ತು (2) ರಿಂದ ನಾವು

∠PQS + ∠PQR = ∠PRT + ∠PRQ ಎಂದು ಸಾಧಿಸಬಹುದು

ಆದರೆ ∠PQR = ∠PRQ [ಕೊಟ್ಟಿರುವಂತೆ]

∴ ∠PQS = ∠PRT

---

4. ಕೆಳಗಿನ ಚಿತ್ರದಲ್ಲಿ x + y = w + z ಆದರೆ AOB ಒಂದು ಸರಳರೇಖೆ ಎಂದು ಸಾಧಿಸಿ.

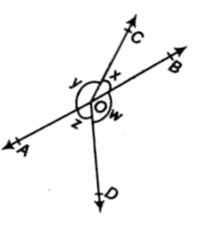
ಕೊಟ್ಟಿರುವಂತೆ : x + y = z + w

ಸಾಧಿಸಬೇಕಾಗಿರುವುದು: ∴ AOB ಒಂದು ಸರಳರೇಖೆ ಎಂದು

ಪುರಾವೆ: ‘O’ ಬಿಂದುವಿನ ಸುತ್ತಲಿನ ಎಲ್ಲ ಕೋನಗಳ ಒಟ್ಟು ಮೊತ್ತ = 360°

x+ y+ z + w = 360⁰ [ಪೂರ್ಣ ಕೋನ]

x + y + x + y = 360⁰ [x + y = z + w]

2x + 2y = 360⁰

2(x + y) = 360⁰

(x + y) =360⁰/2

(x + y) = 180⁰

ಸರಳಯುಗ್ಮ ಆಧಾರ ಪ್ರತಿಜ್ಞೆಗಳು ಸಾಧಿಸುವಂತೆ AOB  ಒಂದು ಸರಳರೇಖೆಯಾಗಿದೆ.

---

5. ಕೊಟ್ಟಿರುವ ಚಿತ್ರದಲ್ಲಿ POQ ಒಂದು ಸರಳರೇಖೆ, OR ಕಿರಣವು PQ ಸರಳರೇಖೆಗೆ ಲಂಬವಾಗಿದೆ. OP ಮತ್ತು OR ಕಿರಣಗಳ ನಡುವೆ OS ಕಿರಣ ಇದೆ.

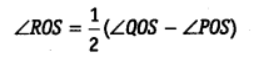
ಎಂದು ಸಾಧಿಸಿ.

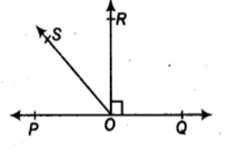
ಕೊಟ್ಟಿರುವಂತೆ : POQ ಒಂದು ಸರಳರೇಖೆಯಾಗಿದೆ.

ಆದರೆ OR ⊥ PQ ∴ ∠ROQ = 90°

⇒ ∠POS + ∠ROS + 90° = 180°

⇒ ∠POS + ∠ROS = 90°

⇒ ∠ROS = 90° – ∠POS … (1)

ಈಗ, ∠ROS + ∠ROQ = ∠QOS

⇒ ∠ROS + 90° = ∠QOS

⇒ ∠ROS = ∠QOS – 90° ……(2)

(1) ಮತ್ತು (2)ನ್ನು ಕೂಡಿಸಿದಾಗ

2 ∠ROS = (∠QOS – ∠POS)

2 ∠ROS = (∠QOS – ∠POS)

∴ ∠ROS =1/2 (∠QOS – ∠POS)

---

 6. ∠XYZ = 64° ಮತ್ತು XY ಯನ್ನು P ವರೆಗೆ ವೃದ್ಧಿಸಿದೆ. ಈ ದತ್ತವನ್ನು ಉಪಯೋಗಿಸಿ ಒಂದು ಚಿತ್ರ ರಚಿಸಿ. ∠ZYP ಯನ್ನು YQ ದ್ವಿಭಾಗಿಸಿದರೆ, ∠XYQ ಮತ್ತು ಸರಳಾಧಿಕ ∠QYP ಕಂಡುಹಿಡಿಯಿರಿ.

ಕೊಟ್ಟಿರುವಂತೆ : ∠XYZ = 64° , ∠ZYP ಯನ್ನು YQ ದ್ವಿಭಾಗಿಸುತ್ತದೆ.

ಸಾಧಿಸಬೇಕಾಗಿರುವುದು : ∠XYQ ಮತ್ತು ಸರಳಾಧಿಕ ∠QYP

ಪರಿಹಾರ :

XYP ಒಂದು ಸರಳರೇಖೆ ಆಗಿದೆ, ಆ ಸರಳರೇಖೆಯ ಮೇಲೆ YQ ಮತ್ತು YZ ಕಿರಣಗಳು ನಿಂತಿವೆ.

∴ ∠XYZ + ∠ZYQ + ∠QYP = 180°

⇒ 64° + ∠ZYQ + ∠QYP = 180° [∠ZYP ಯನ್ನು YQ ದ್ವಿಭಾಗಿಸುತ್ತದೆ, ಆದ್ದರಿಂದ, ∠QYP = ∠ZYQ]

⇒ 2∠QYP = 180° – 64°

⇒ 2∠QYP = 116°

⇒ ∠QYP = “116° ” /2

⇒ ∠QYP = 58°

∴ ಸರಳಾಧಿಕ ∠QYP = 360° – 58° = 302°

∠XYQ = ∠XYZ + ∠ZYQ ಆಗಿರುವುದರಿಂದ

⇒ ∠XYQ = 64° + ∠QYP [∵∠XYZ = 64° (ಕೊಟ್ಟಿರುವಂತೆ) ಮತ್ತು ∠ZYQ = ∠QYP]

⇒ ∠XYQ = 64° + 58°

   = 122° [∠QYP = 58°]

ಆದುದರಿಂದ , ∠XYQ = 122° ಮತ್ತು ಸರಳಾಧಿಕ ∠QYP = 302°.

---

Exercise 3.2

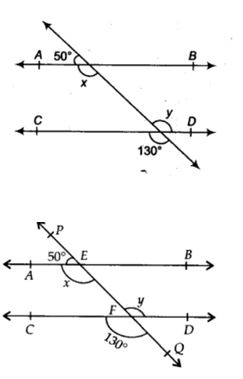
1. ಚಿತ್ರದಲ್ಲಿ x ಮತ್ತು y ಬೆಲೆ ಕಂಡುಹಿಡಿದು AB || CD ಎಂದು ತೋರಿಸಿ.

ಪರಿಹಾರ :

ಚಿತ್ರದಲ್ಲಿ CD ಮತ್ತು PQ ಸರಳರೇಖೆಗಳು ‘F’ ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸುತ್ತಿವೆ .

∴ y = 130° …(1) [ಶೃಂಗಾಭಿಮುಖ ಕೋನಗಳು]

PQ ಒಂದು ಸರಳರೇಖೆಯಾಗಿದೆ ಹಾಗು EA ಕಿರಣವು ಅದರ ಮೇಲೆ ನಿಂತಿದೆ.

∠AEP + ∠AEQ = 180° [ಸರಳಯುಗ್ಮ ಕೋನಗಳು]

50° + x = 180°

⇒ x = 180° – 50°

⇒ x = 130° …(2)

(1) ಮತ್ತು (2) ರಿಂದ x = y = 130°

ಅವು  ಪರ್ಯಾಯ ಅಂತರ್ ಕೋನಗಳು ಆಗಿರುವುದರಿಂದ

∴ AB || CD

---

2. ಚಿತ್ರದಲ್ಲಿ AB || CD, CD || EF ಮತ್ತು y : z =3:7 ಆದರೆ x ಬೆಲೆ ಕಂಡುಹಿಡಿಯಿರಿ.

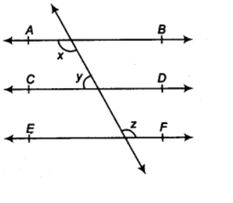
ಕೊಟ್ಟಿರುವಂತೆ : AB || CD, CD || EF ಮತ್ತು y : z = 3 : 7

ಕಂಡುಹಿಡಿಯಬೇಕಾಗಿರುವುದು : x

ಪರಿಹಾರ : AB || CD, ಮತ್ತು CD || EF [ಕೊಟ್ಟಿರುವಂತೆ]

∴ AB || CD || EF

∴ x = z [ಪರ್ಯಾಯ ಅಂತರ್ ಕೋನಗಳು] ….(1)

ದತ್ತಾಂಶದಿಂದ y : z =3 : 7

y ಮತ್ತು z ನಡುವಿನ ಸಾಮಾನ್ಯ ಅನುಪಾತ ‘a’ ಆಗಿರಲಿ
∴ y = 3a ಮತ್ತು z=7a ಆಗುತ್ತದೆ.

ಹಾಗೆಯೇ
x + y = 180°  [ಛೇದಕದ ಒಂದೇ ಪಾರ್ಶ್ವದಲ್ಲಿರುವ ಪ್ರತಿಯೊಂದು ಜೊತೆ ಅಂತರ್ ಕೋನಗಳು ಸರಳಕೋನ ಪೂರಕವಾಗಿರುತ್ತವೆ.]

z + y = 180° [ಸಮೀಕರಣ (1) ರಿಂದ]
7a + 3a = 180°
10a = 180°

a = 180° / 10a = 18°

ಈಗ x = 7a = 7 x 18° = 126°

∴ x = 126°

---

3. ಚಿತ್ರದಲ್ಲಿ AB || CD, EF ⊥ CD ಮತ್ತು ∠GED = 126° ಆದರೆ ∠AGE, ∠GEF ಮತ್ತು ∠FGE ಕಂಡುಹಿಡಿಯಿರಿ.

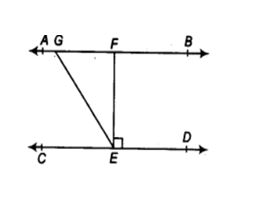
ಕೊಟ್ಟಿರುವಂತೆ : AB || CD, EF ⊥ CD ಮತ್ತು ∠GED = 126°

ಕಂಡುಹಿಡಿಯಬೇಕಾಗಿರುವುದು : ∠AGE, ∠GEF ಮತ್ತು ∠FGE.

ಪರಿಹಾರ : AB || CD ಮತ್ತು GE ಒಂದು ಛೇದಕವಾಗಿದೆ

∴ ∠AGE = ∠GED [ ಪರ್ಯಾಯ ಅಂತರ್ ಕೋನಗಳು]

∠AGE = ∠GED = 126° [ಕೊಟ್ಟಿರುವಂತೆ ]

ಆದರೆ ∠AGE + ∠FGE = 180° [ಸರಳಯುಗ್ಮ ಕೋನಗಳು]

126°+ ∠FGE = 180°

∠FGE = 180° – 126° = 54°

ಆದ್ದರಿಂದ , ∠AGE = 126°, ∠GEF= 36° and ∠FGE = 54°.

---

4. ಚಿತ್ರದಲ್ಲಿ PQ || ST, ∠ PQR = 110° ಮತ್ತು ∠ RST = 130° ಆದರೆ ∠QRS ಕಂಡುಹಿಡಿಯಿರಿ. ( ಸುಳಿವು: R ಬಿಂದುವಿನ ಮೂಲಕ ST ಗೆ ಒಂದು ಸಮಾಂತರ ರೇಖೆಯನ್ನು ಎಳೆಯಿರಿ).

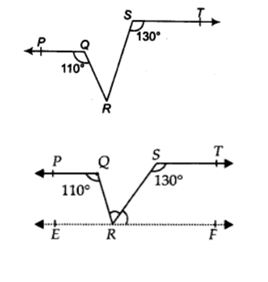
ಕೊಟ್ಟಿರುವಂತೆ : PQ || ST, ∠ PQR = 110° and ∠ RST = 130°

ಕಂಡುಹಿಡಿಯಬೇಕಾಗಿರುವುದು : ∠QRS.

ಕಂಡುಹಿಡಿಯಬೇಕಾಗಿರುವುದು: R ಬಿಂದುವಿನ ಮೂಲಕ ST ಗೆ ಒಂದು ಸಮಾಂತರ ರೇಖೆ EF ಅನ್ನು ಎಳೆಯಿರಿ

ಕೊಟ್ಟಿರುವಂತೆ PQ || ST ಮತ್ತು EF || ST

∴ PQ || EF ಮತ್ತು QR ಒಂದು ಛೇದಕ ರೇಖೆಯಾಗಿದೆ

⇒ ∠PQR = ∠QRF [ಪರ್ಯಾಯ ಅಂತರ್ ಕೋನಗಳು]

ಆದರೆ ∠PQR = 110° [ದತ್ತ ]
∴∠QRF = ∠QRS + ∠SRF = 110° …(1)
ಹಾಗೆಯೇ ST || EF ಮತ್ತು RS ಒಂದು ಛೇದಕ ರೇಖೆಯಾಗಿದೆ

∴ ∠RST + ∠SRF = 180° [ಸರಳಯುಗ್ಮ ಕೋನಗಳು]  

  130° + ∠SRF = 180°⇒ ∠SRF = 180° – 130° = 50°

⇒ ∠QRS = 110° – 50° = 60°

ಹೀಗಾಗಿ , ∠QRS = 60°.

---

5. ಚಿತ್ರದಲ್ಲಿ AB || CD, ∠APQ = 50° ಮತ್ತು ∠PRD = 127° ಆದರೆ x ಮತ್ತು y ಗಳ ಬೆಲೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.

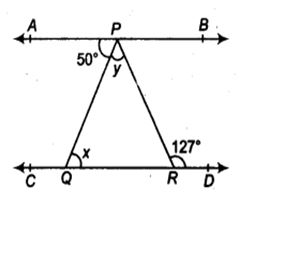
ಕೊಟ್ಟಿರುವುದು : AB || CD, ∠APQ = 50° ಮತ್ತು ∠PRD = 127°,

ಕಂಡುಹಿಡಿಬೇಕಾದುದು : x ಮತ್ತು y.

ಪರಿಹಾರ : AB || CD ಮತ್ತು PQ ಒಂದು ಛೇದಕ ರೇಖೆಯಾಗಿದೆ

∴ ∠APQ = ∠PQR    [ಪರ್ಯಾಯ ಅಂತರ್ ಕೋನಗಳು]

⇒ 50° = x [ ∵ ∠APQ = 50° (ದತ್ತ / ಕೊಟ್ಟಿರುವಂತೆ)]

AB || CD ಮತ್ತು PR ಒಂದು ಛೇದಕ ರೇಖೆಯಾಗಿದೆ
∴ ∠APR = ∠PRD [ಪರ್ಯಾಯ ಅಂತರ್ ಕೋನಗಳು]

⇒ ∠APR = 127° [ ∵ ∠PRD = 127° (ದತ್ತ)]

⇒ ∠APQ + ∠QPR = 127°
⇒ 50° + y = 127° [ ∵ ∠APQ = 50° (ದತ್ತ)]
⇒ y = 127°- 50° = 77°
ಹೀಗೆ x = 50° ಮತ್ತು y = 77°

---

6. ಚಿತ್ರದಲ್ಲಿ PQ ಮತ್ತು RS ಪರಸ್ಪರ ಸಮಾಂತರವಾಗಿರುವ ಎರಡು ದರ್ಪಣಗಳನ್ನು ಇಡಲಾಗಿದೆ. AB ಪತನ ಕಿರಣವು PQ ದರ್ಪಣವನ್ನು B ಬಿಂದುವಿನಲ್ಲಿ ತಾಗಿ ಪ್ರತಿಫಲಿತ ಕಿರಣವು, BC ಹಾದಿಯಲ್ಲಿ ಚಲಿಸಿ RS ದರ್ಪಣವನ್ನು C ಬಿಂದುವಿನಲ್ಲಿ ತಾಗಿ ಪುನಃ CD ಹಾದಿಯಲ್ಲಿ ಪ್ರತಿಫಲಿಸುತ್ತದೆ. AB || CD ಎಂದು ಸಾಧಿಸಿ.

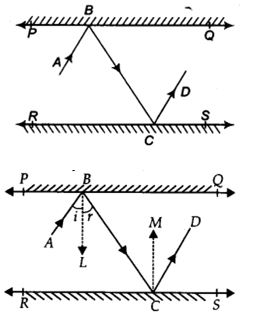
ರಚನೆ : BL ⊥PQ ಮತ್ತು CM ⊥ RS ರಚಿಸಿ
ಪರಿಹಾರ : ∵ PQ || RS ⇒ BL || CM  [∵ BL ⊥ PQ ಮತ್ತು CM ⊥ RS]
ಈಗ , BL || CM ಹಾಗೂ BC ಒಂದು ಛೇದಕ ರೇಖೆಯಾಗಿದೆ

∴ ∠LBC = ∠MCB …(1) [ಪರ್ಯಾಯ ಅಂತರ್ ಕೋನಗಳು]
ಬೆಳಕಿನ ಪ್ರತಿಫಲನ ನಿಯಮದಂತೆ , ಪತನ ಕಿರಣ ಕೋನ = ಪ್ರತಿಫಲಿತ ಕಿರಣ ಕೋನ
∠ABL = ∠LBC ಮತ್ತು ∠MCB = ∠MCD
⇒ ∠ABL = ∠MCD …(2) [ಸಮೀಕರಣ 1 ರಿಂದ ]

(1) ಮತ್ತು (2) ನ್ನು ಕೂಡಿಸಿದಾಗ

∠LBC + ∠ABL = ∠MCB + ∠MCD
⇒ ∠ABC = ∠BCD

ಆದರೆ, ಪ್ರತಿಯೊಂದು ಜೊತೆ ಪರ್ಯಾಯ ಅಂತರ್ ಕೋನಗಳು ಸಮವಾಗಿರುತ್ತವೆ

∴ AB || CD.

---

Exercise 3.2

ತ್ರಿಭುಜದ ಕೋನಗಳ ಮೊತ್ತದ ಗುಣಲಕ್ಷಣ :

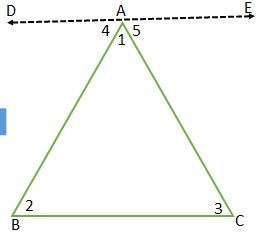
STATEMENT: The sum of the angles of a triangle is 180º.

Given: A  Δ ABC.

To Prove:  ∠1 + ∠2 + ∠3 = 180°

Construction:  Let us draw a line DAE  parallel to BC.

Proof: Statement Reason

DAE ||BC and PQ and AB Is the transversal

Hence, ∠4 = ∠2 (alternate interior angles)

  DAE ||BC and AC Is the transversal (alternate interior angles

  ∠5 = ∠3

Now, DAE is a straight line

∠4 + ∠1 +∠5 = 180°

⇒ ∠1 + ∠4 +∠5 = 180°

Angles on the same side

of DAE at the point A

∠4 = ∠2  and  ∠5 = ∠3

Hence, the sum of the angles of a triangles 180°

---

Exterior angle property of a triangle theorem

STATEMENT: If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.

Given: A  Δ  ABC. whose side BC has been produced to D.

  Forming exterior angle ∠ACD

To Prove:  ∠ACD = ∠BAC + ∠CBA  [∠4 = ∠1 + ∠2

Proof:. Statement Reason

We know that Δ  ABC from the angle sum property

 ∠1 + ∠2 + ∠3 = 180°…..(i)

Also   ∠3 +∠4 = 180°…..(ii) form a linear pair

From equation (i) and (ii) it follows that:

∠3 +∠4 = ∠1 + ∠2 + ∠3

∴ ∠4 = ∠1 + ∠2

Hence, proved

---

1. In figure, sides QP and RQ of ∆PQR are produced to points S and T,   respectively. If ∠SPR = 135° and ∠PQT = 110°, find ∠PRQ.

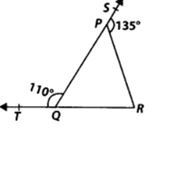
Given:  ∠SPR = 135° and ∠PQT = 110°,

To find: ∠PRQ.

Solution:We have, ∠TQP + ∠PQR = 180°  [Linear pair]

⇒ 110° + ∠PQR = 180°
⇒ ∠PQR = 180° – 110° = 70°

Since, the side QP of ∆PQR is produced to S.

⇒ ∠PQR + ∠PRQ = 135°
[Exterior angle property of a triangle]

⇒ 70° + ∠PRQ = 135° [∠PQR = 70°]
⇒ ∠PRQ = 135° – 70° ⇒ ∠PRQ = 65°

---

2. In figure, ∠X = 62°, ∠XYZ = 54°, if YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ∆XYZ, find ∠OZY and ∠YOZ.

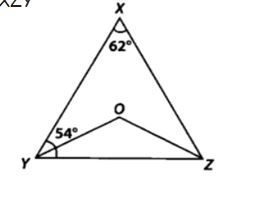
Given: ∠X = 62°, ∠XYZ = 54°, YO and ZO are the bisectors of ∠XYZ and ∠XZY

To find:∠OZY and ∠YOZ.

Solution:In ∆XYZ, we have ∠XYZ + ∠YZX + ∠ZXY = 180°
[Angle sum property of a triangle]

But ∠XYZ = 54° and ∠ZXY = 62°

∴ 54° + ∠YZX + 62° = 180°

⇒ ∠YZX = 180° – 54° – 62° = 64°

YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively.

∴ ∠OYZ = ∠XYZ/ 2 = 54°/ 2 = 27°
and ∠OZY = ∠YZX / 2 = 64°/ 2 = 32°

in ∆OYZ, we have
∠YOZ + ∠OYZ + ∠OZY = 180° [Angle sum property of a triangle

⇒ ∠YOZ + 27° + 32° = 180°
⇒ ∠YOZ = 180° -27° – 32° = 121°

Thus, ∠OZY = 32° and ∠YOZ = 121°

---

3. In figure, if AB || DE, ∠BAC = 35° and ∠CDE = 53°  , find ∠DCE.

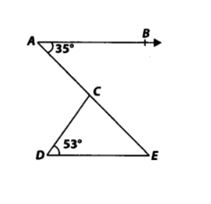
Given: AB || DE, ∠BAC = 35° and ∠CDE = 53°

To find: ∠DCE.

Solution:AB || DE and AE is a transversal.
So, ∠BAC = ∠AED  [Alternate interior angles]

and ∠BAC = 35° [Given]
     ∴ ∠AED = 35°

 in ∆CDE, we have

 ∠CDE + ∠DEC + ∠DCE = 180°     [Angle sum property of a triangle]

∴ 53° + 35° + ∠DCE =180°[∵ ∠DEC = ∠AED = 35° and∠CDE = 53° (Given)]

⇒ ∠DCE = 180° – 53° – 35° = 92°
Thus, ∠DCE = 92°

---

4. In figure, if lines PQ and RS intersect at point T, such that ∠ PRT = 40°, ∠ RPT = 95° and

∠TSQ = 75°, find ∠ SQT.

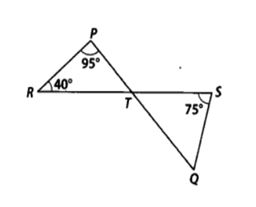
Given: ∠PRT = 40°, ∠ RPT = 95° and ∠TSQ = 75°  

To find: ∠SQT.

Solution:

In ∆PRT, we have ∠P + ∠R + ∠PTR = 180°[Angle sum property of a triangle]

⇒ 95° + 40° + ∠PTR =180° [ ∵ ∠P = 95°, ∠R = 40° (given)]

⇒ ∠PTR = 180° – 95° – 40° = 45°
But PQ and RS intersect at T.

∴ ∠PTR = ∠QTS [Vertically opposite angles

∴ ∠QTS = 45° [ ∵ ∠PTR = 45°]

in ∆ TQS, we have ∠TSQ + ∠STQ + ∠SQT = 180° [Angle sum property of a triangle]

∴ 75° + 45° + ∠SQT = 180° [ ∵ ∠TSQ = 75° and ∠STQ = 45°]

⇒ ∠SQT = 180° – 75° – 45° = 60°
Thus, ∠SQT = 60°

---

5. In figure, if PQ ⊥ PS, PQ||SR, ∠SQR = 2S° and ∠QRT = 65°, then find the values of x and y.

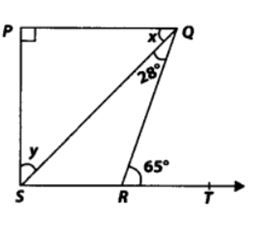
Given

To find:

Solution: In ∆ QRS, the side SR is produced to T.

∴ ∠QRT = ∠RQS + ∠RSQ [Exterior angle property of a triangle]

But ∠RQS = 28° and ∠QRT = 65°

So, 28° + ∠RSQ = 65°
⇒ ∠RSQ = 65° – 28° = 37°

Since, PQ || SR and QS is a transversal.

∴ ∠PQS = ∠RSQ = 37° [Alternate interior angles]

⇒ x = 37°

PQ ⊥ PS ⇒ AP = 90°
 in ∆PQS, ∠P + ∠PQS + ∠PSQ = 180° [Angle sum property of a triangle]

⇒ 90° + 37° + y = 180°

⇒ y = 180° – 90° – 37° = 53°

Thus, x = 37° and y = 53°

---

6. In figure, the side QR of ∆PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR

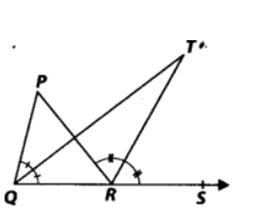
Solution:In ∆PQR, side QR is produced to S, so by exterior angle property, ∠PRS = ∠P + ∠PQR

⇒ 1/2∠PRS = 1/2∠P + 12∠PQR

Now⇒ ∠TRS = 1/2∠P + ∠TQR …(1)[∵ QT and RT are bisectors of ∠PQR and   ∠PRS respectively.]

∠TRS = ∠TQR + ∠T …(2)[Exterior angle property of a triangle]

From (1) and (2),

we have ∠TQR + 1/2∠P = ∠TQR + ∠T

⇒ 1/2∠P = ∠T

⇒ 1/2∠QPR = ∠QTR or ∠QTR = 1/2∠QPR