Summary of polygon

Solved exercise polygon

Summary

POLYGONS:A simple closed curve made up of only line segments is called a polygon. polygon comes from Greek word poly means “”many gon means Ängle”. Polygons are two dimensional shapes made up of straight lines and shapes is closed (all the lines connect up).

Curves that are polygons.

Curves that are not polygons

Classification of polygons

Diagonals

A diagonal is a line segment connecting two non consecutive vertices of a polygon.

Interior and exterior

Simple and complex polygons.

A simple polygon has only one boundary and the sides do not cross each other wise it is a complex polygon.

Simple polygon

Complex polygon

Complex polygon is a polygon whose sides cross over each other one or more times

Concave and convex polygons

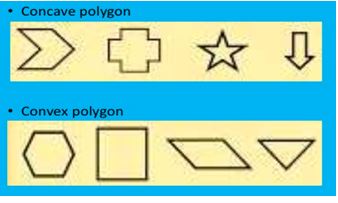
A convex polygon has no internal angle more than 180⁰ and there are any internal angles greater than a straight angle, then it is a concave polygon.

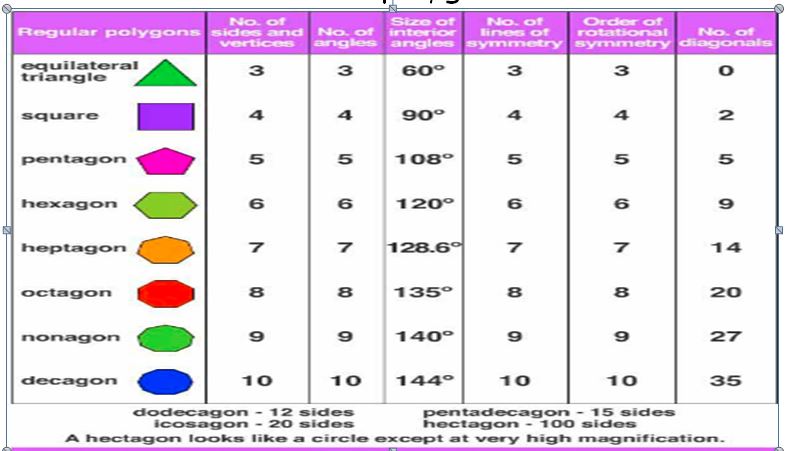
Regular polygons

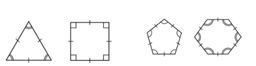
A regular polygon is both equiangular and equilateral.

For Ex:  A square has sides of equal length and angles of equal measure. Hence it is a regular polygon.

Irregular polygon.

A rectangle is equiangular but not equilateral. Hence it is not a regular polygon. It’s called an irregular polygon.

Exercise 4.1

1.Here are some given given figures classify each of them on the basis of their following.

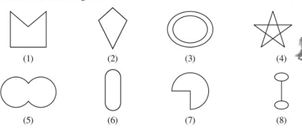
Ans:1)Simple curve

2)simple closed curve

3)Polygon

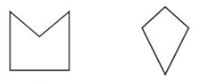
4)Convex polygon

5)Concave polygon.

2. How many diagonals does each of the following have?

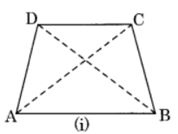
a) A convex quadrilateral

 (i) ABCD is a convex quadrilateral which has two diagonals AC and BD.

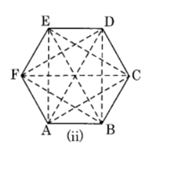
(b) A regular hexagon

ABCDEF is a regular hexagon which has nine diagonals AE, AD, AC, BF, BE, BD, CF, CE and DF.

(c) A triangle

ABC is a triangle which has no diagonal

3. What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and verify)

Solution:In the given figure, we have a quadrilateral ABCD. Join AC diagonal which divides the quadrilateral into two triangles ABC and ADC.

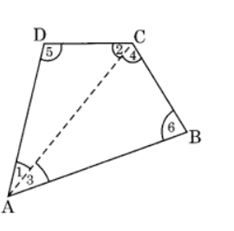
In ∆ABC, ∠3 + ∠4 + ∠6 = 180°…(i) (angle sum property)

In ∆ADC, ∠1 + ∠2 + ∠5 = 180° …(ii) (angle sum property)

Adding, (i) and (ii)

∠1 + ∠3 + ∠2 + ∠4 + ∠5 + ∠6 = 180° + 180°

⇒ ∠A + ∠C + ∠D + ∠B = 360°

Hence, the sum of all the angles of a convex quadrilateral = 360°.

A non-convex quadrilateral

Yes, this property also holds true for a non-convex quadrilateral

Examine the table. (Each figure is divided into triangles and the sum of the angles reduced from that).

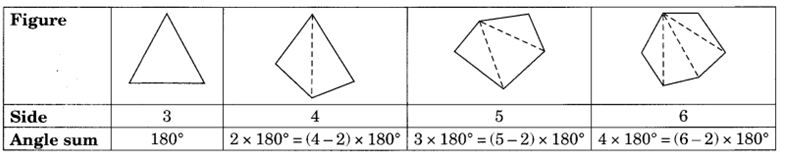
What can you say about the angle sum of a convex polygon with number of sides?
(a) 7
(b) 8
(c) 10
(d) n

Solution:
From the above table, we conclude that the sum of all the angles of a polygon of side ‘n’
= (n – 2) × 180°

(a) Number of sides = 7
Angles sum = (7 – 2) × 180° = 5 × 180°=900⁰

b) Number of sides = 8
Angle sum = (8 – 2) × 180° = 6 × 180°=1080⁰

d) Number of sides = n
Angle sum = (n – 2) × 180°

5. What is a regular polygon? State the name of a regular polygon of
(i) 3 sides
(ii) 4 sides
(iii) 6 sides

Solution:
A polygon with equal sides and equal angles is called a regular polygon.

(i) Equilateral triangle

(ii) Square

(iii) Regular Hexagon

6. Find the angle measure x in the following figures:

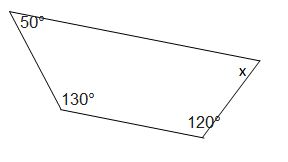
Solution:
(a) Angle sum of a quadrilateral = 360°

⇒ 50° + 130° + 120° + x = 360°

⇒ 300° + x = 360°

⇒ x = 360° – 300° = 60°

X = 60°

(b) Angle sum of a pentagon = 540°

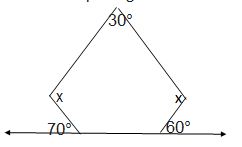
⇒ 30° + x + 110° + 120° + x = 540° [∵ 180° – 70° = 110°; 180° – 60° = 120°]

⇒ 2x + 260° = 540°

⇒ 2x = 540° – 260°

⇒ 2x = 280°

⇒ x = 140°

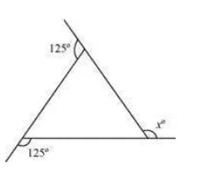
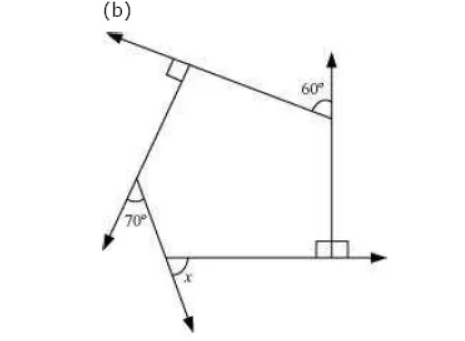
7. (a) Find x + y + z

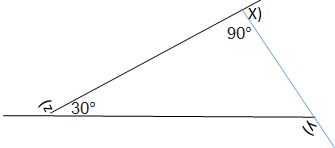
Solution:
(a) ∠a + 30° + 90° = 180° [Angle sum property]

⇒ ∠a + 120° = 180°

⇒ ∠a = 180° – 120° = 60°

Now, y = 180° – a (Linear pair)

⇒ y = 180° – 60°

⇒ y = 120°

and, z + 30° = 180° [Linear pair]

⇒ z = 180° – 30° = 150°

also, x + 90° = 180° [Linear pair]

⇒ x = 180° – 90° = 90°

Thus x + y + z = 90° + 120° + 150° = 360°

Sum of the measures of the exterior angles of a polygon  = 360⁰

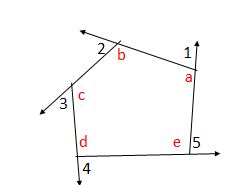
Sum of the two angles in linear pair = 180⁰

Pentagon has 5 sides

then sum of the interior angle of pentagon= (n-2) x180⁰

           = (5-2) x180⁰

         = 3 x180⁰    = 540⁰

^{measure of each angle = 540/5}       = 108⁰

^{then sum of the linear} pair  = 180⁰ – 108 = 72⁰

we know that sum of all exterior angles of any polygon is 360

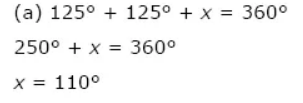
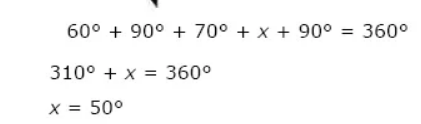
Measure of each exterior angle of a regular polygon = 360/n

Find the measure of each exterior angle of a regular polygon of

i)9 sides

ii)15 sides

Ans:1)Sum of all exterior angles of the given polygon =360⁰          

Each exterior angle of a regular polygon has the same measure.

Thus measure of each exterior angle of a regular polygon of 9 sides

360/9=40

3. How many sides does a regular polygon have if the measure of an exterior angle is 24⁰?      

Sum of all exterior angles of the given polygon is 360⁰/24=15

4. How many sides does a regular polygon have if each its interior angles is 165⁰

180⁰ Regular polygon = all the sides and angles are equal

Let number of sides = n = measure of angles

Sum of interior angles of a regular polygon = (n- 2)x180⁰

165 n = (n- 2)x180⁰

165 n = 180⁰ n – 360

165 n – 180⁰ n = – 360

^– 15 n = – 360

  n = 24 

165 n = (n- 2)x180⁰

165 n = 180⁰ n – 360

165 n – 180⁰ n = – 360

^– 15 n = – 360

  n = 24 

5.a)is it possible to have a regular polygon with measure of each exterior angle is

b)Can it be a regular interior angle of regular polygon?why?

Ans: The sum of all exterior angle of all polygon is 360.Also in a regular polygon each exterior angle is of the same measure. Hence if 360 is a perfect multiple of the given exterior angle then the given polygon will be possible.

a)Exterior angle =22⁰                     

3600 is not a perfect multiple of 22⁰. Hence such polygon is not possible.                              

b)Interior angle =220

Exterior angle = 180⁰-22⁰=158⁰

Such a polygon is not possible as 360⁰ is not a perfect multiple of 158⁰

6. What is the minimum interior angle possible for a regular polygon?

b)what is the maximum exterior angle possible for a regular polygon?

Consider a regular polygon having the lowest possible number of sides(i,e an equilateral triangle).The exterior angle of tthis triangle will be the maximum exterior angle possible for nay rtegular polygon.

Exterior angle of an equilateral triangle=360⁰/3=120⁰

Hence,maximum possible measure of exterior angle for any polygon is        120⁰

we know that an exterior angle and an interior angle are always in a linear pair

Hence, minimum interior angle=180⁰-120⁰=60⁰