Summary of square and square roots

Solved exercise of square roots

Summary

Square Number

When we multiply the number by itself we will get Square number.A square number is a natural number obtained by multiplying the number it self.

Ex: 6 x 6 =36

      5 x 5 = 25

      7 x 7 = 49

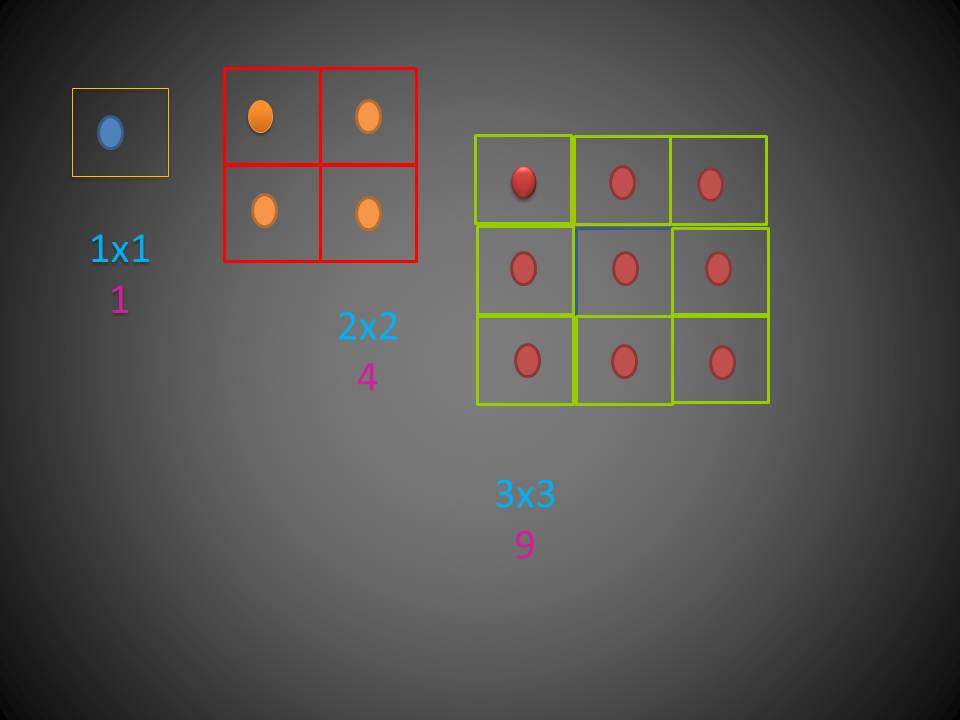
Area of a Square= side X side

• 1 X 1 = 1
• 2 X 2 = 4
• 3 X 3 = 9
• 4 X 4 = 16
• 5 X 5 = 25

Where 5, 6, 7 are the natural numbers and 25,36,49 are the respective square numbers.

If a natural number m can be expressed as n2 , where n is also a natural number, then m is a Square number.

Any integer multiplied to itself gives Perfect Squares.

Eg: 25,36,49

Non perfect squares: Non perfect squares laying in between perfect squares

Properties of Square Numbers

We can see that the square numbers are ending with 0, 1, 4, 5, 6 or    

 9 only. None of the square number is ending with 2, 3, 7 or 8.

If a number has 1 or 9 in the units

place, then it’s square ends in 1.

1	1
9	81
11	121
19	361
21	441

Some More Interesting Patterns

Adding Triangular Numbers

If we could arrange the dotted pattern of the numbers in a triangular form then these numbers are called Triangular Numbers.

Eg: 1, 3, 6, 10…………

If we add two consecutive triangular numbers then we can get the square number.

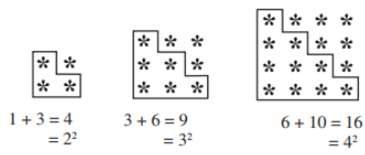
2. Numbers between Square Numbers

If we take two consecutive numbers n and n + 1, then there will be (2n) non-perfect square numbers between their squares numbers.

Example

Let’s take n = 5 and 5² = 25

n + 1 = 5 + 1 = 6 and 6² = 36

2n = 2(5) = 10

Adding Odd Numbers

Sum of first n natural odd numbers is n².

Any square number must be the sum of consecutive odd numbers starting from 1.

And if any natural number which is not a sum of successive odd natural numbers starting with 1, then it will not be a perfect square.

4. A Sum of Consecutive Natural Numbers

Every square number is the summation of two consecutive positive natural numbers.

If we are finding the square of n the to find the two consecutive natural numbers we can use the formula.

5. The Product of Two Consecutive Even or Odd Natural Numbers

If we have two consecutive odd or even numbers (a + 1) and (a -1) then their product will be (a²– 1)

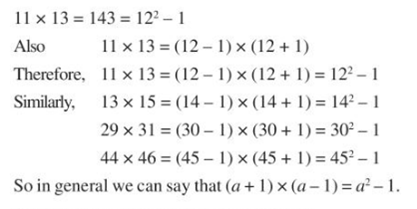
6. Some More Interesting Patterns about Square Numbers

Exercise 5.1

1. What will be the unit digit of the squares of the following numbers?

(i) 81 (ii) 272 (iii) 799 (iv) 3853 (v) 1234 (vi) 20387 (vii) 52698 (viii) 99880 (ix) 12796
(x) 55555

Solution

(i) Unit digit of 81² = 1

(ii) Unit digit of 272² = 4
(iii) Unit digit of 799² = 1
(iv) Unit digit of 3853² = 9

v) Unit digit of 1234² = 6
(vi) Unit digit of 26387² = 9
(vii) Unit digit of 52698² = 4
(viii) Unit digit of 99880² = 0

ix) Unit digit of 12796² = 6
(x) Unit digit of 55555² = 5

2. The following numbers are not perfect squares. Give reason.

i) 1057 (ii) 23453  (iii) 7928 (iv) 222222 (v) 64000 (vi) 89722 (vii) 222000 (viii) 505050

(i)1057 ends with 7 at unit place. So it is not a perfect square number.

(ii) 23453 ends with 3 at unit place. So it is not a perfect square number.

(iii) 7928 ends with 8 at unit place. So it is not a perfect square number.

(iv) 222222 ends with 2 at unit place. So it is not a perfect square number.

(v) 64000 ends with 3 zeros. So it cannot a perfect square number.

(vi) 89722 ends with 2 at unit place. So it is not a perfect square number.

(vii) 22000 ends with 3 zeros. So it can not be a perfect square number.

(viii) 505050 ends with 1 zero. So it is not a perfect square number.

3. The squares of which of the following would be odd numbers?

(i) 431 (ii) 2826 (iii) 7779  (iv) 82004

(i)431² is an odd number.

(ii) 2826² is an even number.

(iii) 7779² is an odd number.

(iv) 82004² is an even number.

4. Observe the following pattern and find the missing digits

11² = 121
101² = 10201
1001² = 1002001
100001² = 1…2…1
10000001² = ………

Solution

According to the above pattern, we have
100001² = 10000200001
10000001² = 100000020000001

5. Observe the following pattern and supply the missing numbers.

11² = 121
101² = 10201
10101² = 102030201
1010101² = ……….
……….² = 10203040504030201

Solution

According to the above pattern, we have

1010101² = 1020304030201

101010101² = 10203040504030201

6. Using the given pattern, find the missing numbers

1² + 2² + 2² = 3²
2² + 3² + 6² = 7²
3² + 4² + 12² = 13²
4² + 5² + ….² = 21²
5² + ….² + 30² = 31²
6² + 7² + …..² = ……²

Solution

According to the given pattern, we have

4² + 5² + 20² = 21²

5² + 6² + 30² = 31²

6² + 7² + 42² = 43²

7. Without adding, find the sum.

(i) 1 + 3 + 5 + 7 + 9
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23

Solution:

We know that the sum of n odd numbers = n²

(i)1 + 3 + 5 + 7 + 9 = (5)² = 25 [∵ n = 5]

(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = (10)² = 100 [∵ n = 10]

(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 = (12)² = 144 [∵ n = 12]

8. (i) Express 49 as the sum of 7 odd numbers.
(ii) Express 121 as the sum of 11 odd numbers.

Solution:
(i) 49 = 1 + 3 + 5 + 7 + 9 + 11 + 13 (n = 7)

(ii) 121 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 (n = 11)

9. How many numbers lie between squares of the following numbers?
(i) 12 and 13
(ii) 25 and 26
(iii) 99 and 100.

Solution:

i)We know that numbers between n² and (n + 1)² = 2n

Numbers between 12² and 13² = (2n) = 2 × 12 = 24

ii) Numbers between 25² and 26² = 2 × 25 = 50 (∵ n = 25)

(iii) Numbers between 99² and 100² = 2 × 99 = 198 (∵ n = 99)