Algebraic Expression and Identities
Summary of algebraic expression and Identities
Solved exercise of algebraic expression and Identities

Summary
A combination of constants and variables connected by the signs of fundamental operations of addition, subtraction, multiplication and division is called an algebraic expression.
Algebraic Expression
A symbol which takes various numerical values is called a variable.Various parts of an algebraic expression which are separated by the signs of ‘+’ or ‘-‘ are called the terms of the expression.
What are Expressions?
We know that a constant is a symbol having fixed numerical value whereas a variable is a symbol assuming various numerical values.
An algebraic expression is formed from variables and constants. A combination of variables and constants connected by the signs +, -, × and ÷ is called an algebraic expression. The variable/variables in an algebraic expression can assume countless different values. The value of algebraic expression changes with the value (s) assumed by the variable (s) it contains.
Algebraic Expression
Any mathematical expression which consists of numbers, variables and operations are called Algebraic Expression.

1. Terms
Every expression is separated by an operation which is called Terms. Like 7n and 2 are the two terms in the above figure.
2. Factors
Every term is formed by the product of the factors.7n is the product of 7 and n which are the factors of 7n.
3. Coefficient
The number placed before the variable or the numerical factor of the term is called Coefficient of that variable.7 is the numerical factor of 7n so 7 is coefficient here.
4. Variable
Any letter like x, y etc. are called Variables. The variable in the above figure is n.
5. Operations
Addition, subtraction etc. are the operations which separate each term.
6. Constant
The number without any variable is constant. 2 is constant here.
Number Line and an Expression
An expression can be represented on the number line.
Example
How to represent x + 5 and x – 5 on the number line?
Solution:
First, mark the distance x and then x + 5 will be 5 unit to the right of x

In the case of x – 5 we will start from the right and move towards the negative side. x – 5 will be 5 units to the left of x.
Monomials, Binomials and Polynomials

An expression that contains exactly one, two or three terms is called a monomial, binomial or trinomial, respectively. In general, an expression containing, one or more terms with non-zero coefficients and with variable having non-negative exponents is called a polynomial.

Like and Unlike Terms
Like (or similar) terms are formed from the same variables and the powers of these variables are also the same. Coefficients of like terms need not be the same. In case otherwise, they are called, unlike (or dissimilar) terms.
Terms having the same variable are called Like Terms.
Examples of Like Terms •2x and -9x •24xy and 5yx •6x2 and 12x2
The terms having different variable are called, Unlike Terms.
Examples of Unlike Terms •2x and – 9y •24xy and 5pq •6x2 and 12y2
Addition and Subtraction of Algebraic Expressions
Steps to add or Subtract Algebraic Expression
•First of all, we have to write the algebraic expressions in different rows in such a way that the like terms come in the same column. •
•Add them as we add other numbers.
•If any term of the same variable is not there in another expression then write is as it is in the solution.
Example
Add 15p2 – 4p + 5 and 9p – 11
Solution:
Write down the expressions in separate rows with like terms in the same column and add.

Example
Subtract 5a2 – 4b2 + 6b – 3 from 7a2 – 4ab + 8b2 + 5a – 3b.
Solution:
For subtraction also write the expressions in different rows. But to subtract we have to change their signs from negative to positive and vice versa.
7a2 – 4ab + 8b2 + 5a – 3b

Multiplication of Algebraic Expressions
While multiplying we need to take care of some points about the multiplication of like and unlike terms.
1. Multiplication of Like Terms The coefficients will get multiplied. •The power will not get multiplied but the resultant variable will be the addition of the individual powers.
Example •The product of 4x and 3x will be 12x2. •The product of 5x, 3x and 4x will be 60x3.
2. Multiplication of Unlike Terms The coefficients will get multiplied. •The power will remain the same if the variable is different. •If some of the variables are the same then their powers will be added.
Example •The product of 2p and 3q will be 6pq •The product of 2x2y, 3x and 9 will be 54x3y
Multiplying a Monomial by a Monomial
1. Multiplying Two Monomials
While multiplying two polynomials the resultant variable will come by •The coefficient of product = Coefficient of the first monomial × Coefficient of the second monomial •The algebraic factor of product = Algebraic factor of the first monomial × Algebraic factor of the second monomial.
Example
25y × 3xy = 125xy2
2. Multiplying Three or More Monomials
While multiplying three or more monomial the criterion will remain the same.
Example
4xy × 5x2y2 × 6x3 y3
= (4 × 5 × 6) × (x × x2 × x3) × (y × y2 × y3)
= 120 x6y6
Multiplying a Monomial by a Polynomial
1. Multiplying a Monomial by a Binomial
To multiply a monomial with a binomial we have to multiply the monomial with each term of the binomial.
Example
•Multiplication of 8 and (x + y) will be (8x + 8y).
•Multiplication of 3x and (4y + 7) will be (12xy + 21x).
•Multiplication of 7x3 and (2x4 + y4) will be (14x7+ 7x3y4).
•Multiplication of 7x3 and (2x4 + y4) will be (14x7+ 7x3y4).
2. Multiplication of Monomial by a trinomial
This is also the same as above
Example
•Multiplication of 8 and (x + y + z) will be (8x + 8y + 8z).
•Multiplication of 4x and (2x + y + z) will be (8x2 + 4xy + 4xz).
•Multiplication of 7x3 and (2x4+ y4+ 2) will be (14x7 + 7x3y4 + 14x3).
Multiplying a Polynomial by a Polynomial
1. Multiplying a Binomial by a Binomial
We use the distributive law of multiplication in this case. Multiply each term of a binomial with every term of another binomial. After multiplying the polynomials we have to look for the like terms and combine them.
Example:Simplify (3a + 4b) × (2a + 3b)
Solution:
(3a + 4b) × (2a + 3b)
= 3a × (2a + 3b) + 4b × (2a + 3b) [distributive law]
= (3a × 2a) + (3a × 3b) + (4b × 2a) + (4b × 3b)
= 6 a2 + 9ab + 8ba + 12b2
= 6 a2 + 17ab + 12b2 [Since ba = ab]
2. Multiplying a Binomial by a Trinomial
In this also we have to multiply each term of the binomial with every term of trinomial.
Example:Simplify (p + q) (2p – 3q + r) – (2p – 3q) r.
Solution:
We have a binomial (p + q) and one trinomial (2p – 3q + r)
(p + q) (2p – 3q + r)
= p(2p – 3q + r) + q (2p – 3q + r)
= 2p2 – 3pq + pr + 2pq – 3q2 + qr
= 2p2 – pq – 3q2 + qr + pr (–3pq and 2pq are like terms)
(2p – 3q) r = 2pr – 3qr
(p + q) (2p – 3q + r) – (2p – 3q) r
= 2p2 – pq – 3q2 + qr + pr – (2pr – 3qr)
= 2p2 – pq – 3q2 + qr + pr – 2pr + 3qr
= 2p2 – pq – 3q2 + (qr + 3qr) + (pr – 2pr)
= 2p2 – 3q2 – pq + 4qr – pr
Identities
An identity is an equality which is true for every value of the variable but an equation is true for only some of the values of the variables.
So an equation is not an identity.
Like, x2 = 1, is valid if x is 1 but is not true if x is 2.so it is an equation but not an identity.
Some of the Standard Identities
(a + b)2 = a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2
a2 – b2 = (a + b) (a – b)
(x + a) (x + b) = x2 + (a + b)x + ab
These identities are useful in carrying out squares and products of algebraic expressions. They give alternative methods to calculate products of numbers and so on.
Exercise 6.1 , 6.2 and 6.3
1.Identify the terms, their coefficients for each of the following expressions.
(i)5xyz2 – 3zy (ii) 1 + x + x2 (iii) 4x2y2 – 4x2y2z2 + z2
(iv) 3 – pq + qr – rp (v) x2 + y2 – xy (vi) 0.3a – 0.6ab + 0.5b
Solution:

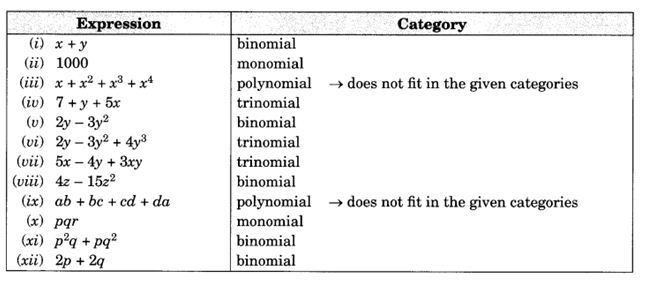
2. Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any of these three categories?
x + y, 1000, x + x2 + x3 + x4, 7 + y + 5x, 2y – 3y2, 2y – 3y2 + 4y3, 5x – 4y + 3xy, 4z – 15z2,
ab + bc + cd + da, pqr, p2q + pq2, 2p + 2q
Solution:
3. Add the following:
i) ab – bc, bc – ca, ca – ab
(ab – bc) + (bc – ca) + (ca – ab) (Adding all the terms)
= ab – bc + bc – ca + ca – ab
= (ab – ab) + (bc – bc) + (ca – ca) (Collecting the like terms together)
= 0 + 0 + 0
= 0
(ii) a – b + ab, b – c + bc, c – a + ac
We have (a – b + ab) + (b – c + bc) + (c – a + ac) (Adding all the terms)
= a – b + ab + b – c + bc + c – a + ac
= (a – a) + (b – b) + (c – c) + ab + bc + ac (Collecting all the like terms together)
= 0 + 0 + 0 + ab + bc + ac
= ab + bc + ac
(iii) 2p2q2 – 3pq + 4, 5 + 7pq – 3p2q2
(Adding columnwise)
By arranging the like terms in the same column, we have

iv) l2 + m2, m2 + n2, n2 + l2, 2lm + 2mn + nl By arranging the like terms in the same column, we have

Thus, the sum of the given expressions is 2(l2 + m2 + n2 + lm + mn + nl)
4. Subtract
(a) Subtract 4a – 7ab + 3b + 12 from 12a – 9ab + 5b – 3
Arranging the like terms column-wise, we have

[Change the signs of all the terms of lower expressions and then add]
(b) Arranging the like terms column-wise, we have

[Change the signs of all the terms of lower expressions and then add]
(c) Arranging the like terms column-wise, we have

[Change the signs of all the terms of lower expressions and then add]
The terms are p2q – 7pq2 + 8pq – 18q + 5p + 20
Exercise 9.2
1. Find the product of the following pairs of monomials.
(i) 4, 7p (ii) -4p, 7p (iii) -4p, 7pq (iv) 4p3, -3p (v) 4p, 0
Solution:
(i)4 × 7p = (4 × 7) × p = 28p
(ii) -4p × 7p = (-4 × 7) × p × p = -28p2
(iii) -4p × 7pq = (-4 × 7) × p × pq = -28p2q
(iv) 4p3 × -3p = (4 × -3) × p3 × p = -12p4
(v) 4p x 0 = (4 × 0) × p = 0 × p = 0
2. Find the areas of rectangles with the following pairs of monomials as their lengths and breadths respectively.
(p, q); (10m, 5n); (20x2, 5y2); (4x, 3x2); (3mn, 4np)
Solution:(i) Length = p units and breadth = q units
Area of the rectangle = length × breadth = p × q = pq sq units
(ii) Length = 10 m units, breadth = 5n units
Area of the rectangle = length × breadth = 10 m × 5 n = (10 × 5) × m × n = 50 mn sq units
iii) Length = 20x2 units, breadth = 5y2 units
Area of the rectangle = length × breadth = 20x2 × 5y2 = (20 × 5) × x2 × y2 = 100x2y2 sq units
(iv) Length = 4x units, breadth = 3x2 units
Area of the rectangle = length × breadth = 4x × 3x2 = (4 × 3) × x × x2 = 12x3 sq units
(v) Length = 3mn units, breadth = 4np units
Area of the rectangle = length × breadth = 3mn × 4np = (3 × 4) × mn × np = 12mn2p sq units
3. Complete the table of Products.

4. Obtain the volume of rectangular boxes with the following length, breadth and height respectively.
i) 5a, 3a2, 7a4 (ii) 2p, 4q, 8r (iii) xy, 2x2y, 2xy2 (iv) a, 2b, 3c
Solution:
(i) Here, length = 5a, breadth = 3a2, height = 7a4
Volume of the box = l × b × h = 5a × 3a2 × 7a4 = 105 a7 cu. units
(ii) Here, length = 2p, breadth = 4q, height = 8r
Volume of the box = l × b × h = 2p × 4q × 8r = 64pqr cu. units
iii) Here, length = xy, breadth = 2x2y, height = 2xy2
Volume of the box = l × b × h = xy × 2x2y × 2xy2 = (1 × 2 × 2) × xy × x2y × xy2 = 4x4y4 cu. units
iv) Here, length = a, breadth = 2b, height = 3c
Volume of the box = length × breadth × height = a × 2b × 3c = (1 × 2 × 3)abc = 6 abc cu. units
5. Obtain the product of
i) xy, yz, zx (ii) a, -a2, a3 (iii) 2, 4y, 8y2, 16y3 (iv) a, 2b, 3c, 6abc (v) m, -mn, mnp
Solution:(i) xy × yz × zx = x2y2z2
(ii) a × (-a2) × a3 = -a6(iii) 2 × 4y × 8y2 × 16y3 = (2 × 4 × 8 × 16) × y × y2 × y3 = 1024y6
(iv) a × 2b × 3c × 6abc = (1 × 2 × 3 × 6) × a × b × c × abc = 36 a2b2c2
(iv) a × 2b × 3c × 6abc = (1 × 2 × 3 × 6) × a × b × c × abc = 36 a2b2c2
(v) m × (-mn) × mnp = [1 × (-1) × 1 ]m × mn × mnp = -m3n2p
Exercise 9.3
1. Carry out the multiplication of the expressions in each of the following pairs:
(i) 4p, q + r (ii) ab, a – b (iii) a + b, 7a2b2 (iv) a2 – 9, 4a (v) pq + qr + rp, 0
Solution:i) 4p × (q + r) = (4p × q) + (4p × r) = 4pq + 4pr
ii) ab, a – b = ab × (a – b) = (ab × a) – (ab × b) = a2b – ab2
iii) (a + b) × 7a2b2 = (a × 7a2b2) + (b × 7a2b2) = 7a3b2 + 7a2b3
(iv) (a2 – 9) × 4a = (a2 × 4a) – (9 × 4a) = 4a3 – 36a
(v) (pq + qr + rp) × 0 = 0 [∵ Any number multiplied by 0 is = 0]
2. Complete the table.

Solution:
(i) a × (b + c + d) = (a × b) + (a × c) + (a × d) = ab + ac + ad
(ii) (x + y – 5) (5xy) = (x × 5xy) + (y × 5xy) – (5 × 5xy) = 5x2y + 5xy2 – 25xy
(iii) p × (6p2 – 7p + 5) = (p × 6p2) – (p × 7p) + (p × 5) = 6p3 – 7p2 + 5p
(iv) 4p2q2 × (p2 – q2) = 4p2q2 × p2 – 4p2q2 × q2 = 4p4q2 – 4p2q4
(v) (a + b + c) × (abc) = (a × abc) + (b × abc) + (c × abc) = a2bc + ab2c + abc2
3. Find the products.
4. (a) Simplify: 3x(4x – 5) + 3 and find its values for (i) x = 3 (ii) x = 1/2.
(b) Simplify: a(a2 + a + 1) + 5 and find its value for (i) a = 0 (ii) a = 1 (iii) a = -1
Solution:
(a) We have 3x(4x – 5) + 3 = 4x × 3x – 5 × 3x + 3 = 12x2 – 15x + 3
i) For x = 3, we have
12 × (3)2 – 15 × 3 + 3 = 12 × 9 – 45 + 3 = 108 – 42 = 66
(b) We have a(a2 + a + 1) + 5
= (a2 × a) + (a × a) + (1 × a) + 5
= a3 + a2 + a + 5
(i) For a = 0, we have
= (0)3 + (0)2 + (0) + 5 = 5
(ii) For a = 1, we have
= (1)3 + (1)2 + (1) + 5
= 1 + 1 + 1 + 5 = 8
(iii) For a = -1, we have
= (-1)3 + (-1)2 + (-1) + 5
= -1 + 1 – 1 + 5 = 4.
5. (a) Add: p(p – q), q(q – r) and r(r – p)
(b) Add: 2x(z – x – y) and 2y(z – y – x)
(c) Subtract: 3l(l – 4m + 5n) from 4l(10n – 3m + 2l)
(d) Subtract: 3a(a + b + c) – 2b(a – b + c) from 4c(-a + b + c)
Solution:
(a) p(p – q) + q(q – r) + r(r – p)
= (p × p) – (p × q) + (q × q) – (q × r) + (r × r) – (r × p)
= p2 – pq + q2 – qr + r2 – rp
= p2 + q2 + r2 – pq – qr – rp
(b) 2x(z – x – y) + 2y(z – y – x)
= (2x × z) – (2x × x) – (2x × y) + (2y × z) – (2y × y) – (2y × x)
= 2xz – 2x2 – 2xy + 2yz – 2y2 – 2xy
= -2x2 – 2y2 + 2xz + 2yz – 4xy
= -2x2 – 2y2 – 4xy + 2yz + 2xz
(c) 4l(10n – 3m + 2l) – 3l(l – 4m + 5n)
= (4l × 10n) – (4l × 3m) + (4l × 2l) – (3l × l) – (3l × -4m) – (3l × 5n)
= 40ln – 12lm + 8l2 – 3l2 + 12lm – 15ln
= (40ln – 15ln) + (-12lm + 12lm) + (8l2 – 3l2)
= 25ln + 0 + 5l2
= 25ln + 5l2
= 5l2 + 25ln
(d) [4c(-a + b + c)] – [3a(a + b + c) – 2b(a – b + c)]
= (-4ac + 4bc + 4c2) – (3a2 + 3ab + 3ac – 2ab + 2b2 – 2bc)
= -4ac + 4bc + 4c2 – 3a2 – 3ab – 3ac + 2ab – 2b2 + 2bc
= -3a2 – 2b2 + 4c2 – ab + 6bc – 7ac